Exercise 2.1 - 8-Puzzle

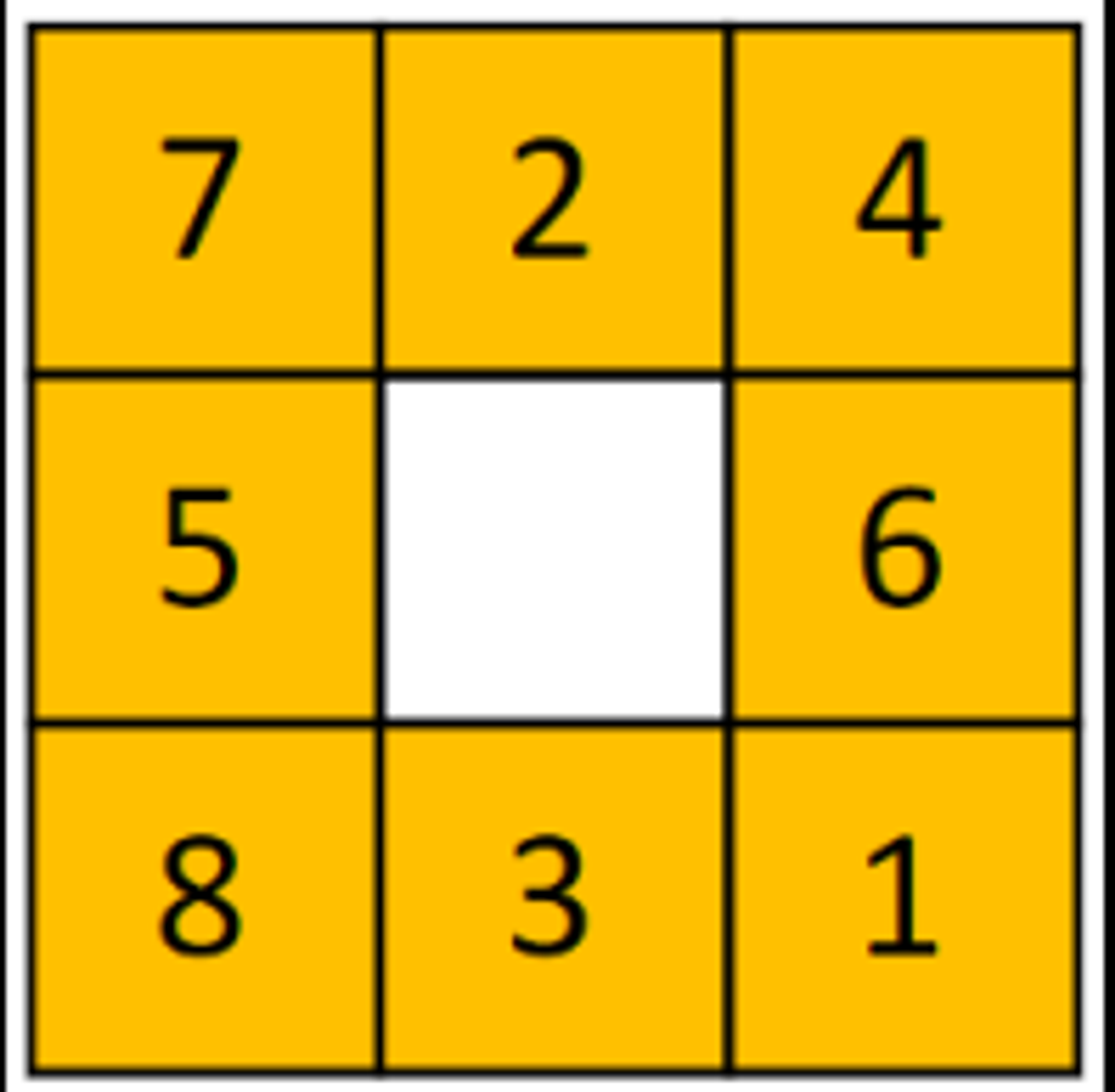
Strategy for a 8-Puzzle Solver.

Problem Representation

• Define the Agent Design Components
• Implement a State class
• Implement a get_successors(...) method to get potential future steps.

Search Algorithm

• Search Node Class (Container Entry)
• Implement Breadth-First Search (BFS) and Depth-First Search (DFS)

Agent Design Components

State Space

• All possible combinations of tile positions (both numbered and blank tiles)

  $$S = \{\{t_0, t_1, ..., t_8\}, where\ t_i \in [\_, 1, 2, 3, 4, 5, 6, 7, 8] \}$$

• Each value of $i$ corresponds to a grid position (ordered left to right, top to bottom)

• Not a compact representation → Duplicates and unreachable states can be represented

• As a result of this, we want to avoid enumerating states / constructing an explicit state graph

Action Space

• Swap the blank tile with an adjacent numbered tile

• Not all actions are valid in every state (e.g. borders)

World Dynamics

• Position of blank tile and position of adjacent tile in selected direction are swapped.
• $i_{blank} \leftarrow i_{adjacent}, i_{adjacent} \leftarrow i_{blank}$ (to perform this operation, a temporary variable is needed)

Utility Function

• $U(s)=1$ if current state is the goal state,

                  $0$ otherwise
  

• The tile in every position matches between the current state and the goal

State Class

A constructor (__init__)

• Create either from a string or list
• Index of blank tile as an instance variable (to avoid repeated computation)
• Use strings as they are immutable in Python

class EightPuzzle:
	def __init__(self, squares):
		if type(squares) is str:
			self.squares == list(squares)
		else:
			# Convert the list to string
			self.squares = [str(i) for i in squares]

			# Find position of _
			idx = -1
			for i in range(len(self.squares)):
				if self.squares[i] == '_':
					idx = i;
			self.idx = idx

Equality (__eq__)

• Given another object (instance of EightPuzzle class), test if it is the same as this object.
• This is also required when using the '==' operator, or in keyword.
• Required to check if a state has been visited before (i.e. is in a visited collection)
• If we want to make the __eq__ function more rigorous, we could test for type.
• This isn't done in the example as it is additional computation, and this case isn't used in the implementation.

def __eq__(self, obj):;
		if obj is None:
				return False
		# optional test for type:
		"""
		if type(obj) != EightPuzzle:
				return False
		"""
		return tuple(self.squares) ==
				tuple(obj.squares)

Hash (__hash__)

• Having a __hash__ method implemented allows a class to be inserted into Hash Table data structures, such as sets and dictionaries

def __hash__(self):
	return hash(tuple(self.squares))

• Rather than iterating through every element in an array, hash tables use the hash value as a memory address - constant time lookup (vs linear time lookup)

• Very important for search performance - we frequently need to check if states have been visited before
  • Sets of visited state can contain 1000s of elements.
• Any immutable datatype will have a built-in __hash__ function
  • Python's built-in hash() function works for any immutable type (integer, float, boolean, string, tuple)
  • Good approach is to convert state variables to an immutable form, combine it in a tuple and use a built-in hash function.
  • Hash value of an object should never change - only implement __hash__ for data types that are immutable.

Finding Successors - get_successors(...)

• Using a consistent format allows environments, algorithms to be reused - use consistent method names and output formats.

• Return a collection of possible next states.

• Must be able to recover the action associated with each next state

• Helper methods for different movement directions (swap tiles in each direction)

• Only return the next state for actions which are valid.

• Valid actions depend on row and column (moving the blank tile up is not possible when the blank tile is in the top row).

• Use the modulo (%) and integer division (//) operators to extract the row and column.

  • row = index // num_cols
  • col = index % num_rows

• Here, set next_state=None if the action is invalid.

• Representing the successors in a dictionary may be more accessible.

def get_successors(self):
  successors = []

  if self.idx % 3 > 0:
    successors.append(self.move_left())
  else:
    successors.append(None)

  if self.idx % 3 < 2:
    successors.append(self.move_right())
  else:
    successors.append(None)

  if self.idx // 3 > 0:
    successors.append(self.move_up())
  else:
    successors.append(None)

  if self.idx // 3 < 2:
    successors.append(self.move_down())
  else:
    successors.append(None)

  return successors

Helper Methods

• Note that in this example, copy.deepcopy() is slower than the deep copy function in the constructor

  new_squares = [str(i) for i in self.squares]

• Use some other rules (functions) to prevent moving to an invalid state - in this case, we use the get_successors() function to do this

  • Valid actions depend on the position (row, col) of the "_" character.

def move_left(self):
	  new_squares = copy.deepcopy(self.squares)
	  new_squares[self.idx] = self.squares[self.idx-1]
	  new_squares[self.idx-1] = self.squares[self.idx]
	  return EightPuzzle(new_squares)

def move_right(self):
	  new_squares = copy.deepcopy(self.squares)
	  new_squares[self.idx] = self.squares[self.idx+1]
	  new_squares[self.idx+1] = self.squares[self.idx]
	  return EightPuzzle(new_squares)

def move_up(self):
	  new_squares = copy.deepcopy(self.squares)
	  new_squares[self.idx] = self.squares[self.idx-3]
	  new_squares[self.idx-3] = self.squares[self.idx]
	  return EightPuzzle(new_squares)

def move_down(self):
	  new_squares = copy.deepcopy(self.squares)
	  new_squares[self.idx] = self.squares[self.idx+3]
	  new_squares[self.idx+3] = self.squares[self.idx]
	  return EightPuzzle(new_squares)

Search Node Class

• We need a way to be able to recover the sequence of actions once the goal node has been found.
• We could store the sequence of actions at each node of the search tree (space intensive)
• We could alternatively store the parent of each node
• It's best to avoid keeping a list of actions inside the state class itself - creates equality check mutability issues
  • What if there are two states that have the same arrangement of tiles, but different steps to get there?
  • They're equal (in position of tiles) yet the state variables (in this case, sequence of steps) aren't the same.
• Don't need equality or hash function (store only the state in visited set).
• Use an alternative get_successors pattern:
  • The state class contains a list of actions (State.ACTIONS)
  • Method to perform actions (perform_action(action)) → next_state
  • Equality and Hash method

class ContainerEntry:
	def __init__(self, puzzle, actions):
	  self.puzzle = puzzle
	  self.actions = actions

	def get_successors(self):
	  s = []
	  suc = self.puzzle.get_successors()

	  if suc[0] is not None:
      s.append(ContainerEntry(suc[0],
				self.actions + [LEFT]))
	  if suc[1] is not None:
      s.append(ContainerEntry(suc[1],
				self.actions + [RIGHT]))
	  if suc[2] is not None:
      s.append(ContainerEntry(suc[2],
				self.actions + [UP]))
	  if suc[3] is not None:
      s.append(ContainerEntry(suc[3],
				self.actions + [DOWN]))

	  return s

	def __eq__(self, obj):
	  return self.puzzle == obj.puzzle

• The search node contains
  • Method get_successors() → collection(SearchNode)
  • For each action in State.ACTIONS, nextState = State.perform_action(action

Search Algorithm

• A generic search algorithm structure is given by:

1. Container = [SearchNode(init_state)]
2. While Container is not Empty:
3. Current_Node ← Choose Node from Container (and remove it)
4. If Current_Node.state is the goal state:

5. Return Current_Node.actions
   

6. Successors ← Current_Node.get_successors()
7. For s in Successors:

8. If s not visited (or s visited at higher cost than current cost)
   

9.   Add SearchNode(s) to the Container
   

10.   Add s to the visited set.
    

• Search type is determined by how the node to remove from the container is chosen
  • For BFS, choose the first/oldest node in the container (FIFO Stack)
  • For DFS, choose the last/newest node in the container (FILO Stack)
  • Note that there is only one (line) of difference between the two algorithms.

# BFS Algorithm
def bfs(initial, goal):
    container = [ContainerEntry(initial, [])]
    visited = set([])

    i = 0
    while len(container) > 0:
        # expand node
        node = container.pop(0)
        if node.puzzle == goal:
            return node.actions

        # add successors
        suc = node.get_successors()
        for s in suc:
            if s.puzzle not in visited:
                container.append(s)
                visited.add(s.puzzle)
        i += 1

    return None

# DFS Algorithm
def dfs(initial, goal):
    container = [ContainerEntry(initial, [])]
    visited = set([])

    i = 0
    while len(container) > 0:
        # expand node
        node = container.pop(-1)
        if node.puzzle == goal:
            return node.actions

        # add successors
        suc = node.get_successors()
        for s in suc:
            if s.puzzle not in visited:
                container.append(s)
                visited.add(s.puzzle)
        i += 1

    return None

Exercise 2.2: Performance Comparison

• Trying to find the difference in computational time to get from state 281_43765 to 1238_4765
  • BFS takes 0.00572 seconds, using 9 actions
  • DFS takes 156.203 seconds, using 59,123 actions
• Trying to find the difference in computational time to get from state 281463_75 to 1238_4765
  • BFS takes 0.01781 seconds, using 12 actions
  • DFS takes 12.53520 seconds, using 27,962 actions
• BFS is much faster than DFS, and also produces solutions with far fewer moves
• Time taken by BFS is proportional to the minimum solution depth
• Time take and number of moves in the solution for DFS depends on the order actions are expanded
• DFS depends on the visited set in order to find solution
• Results match the expected time complexity
• Space complexity isn't tested, but DFS has much better space complexity - the advantage is mitigated by the need for the visited set

Exercise 2.3: Solvability and Parity

• There is no solution for a given 8-Puzzle when the container becomes empty before the goal is reached
• Both BFS and DFS can identify no solution as long as a visited set is maintained.
• Traversing the entire state space to identify that no solution exists is very time consuming, so we can use parity to check for solvability

Parity

• Each state can be assigned either odd or even parity
• In the 8-Puzzle problem, parity is invariant (i.e. doesn't change) for all available (valid) moves
  • So, for a solution between two states, to exist, parity(initial) == parity(goal)
• For a solution to exist, both the initial and goal state must have the same parity
• Parity match is both necessary (and sufficient) for a solution to exist

Number of Inversions

• The number of inversions is given by the number of tiles which are out of place relative to _12345678
  • N(s, 7) = 6 (out of place w.r.t 2, 4, 5, 6, 3, 1)
  • N(s, 2) = 1 (out of place w.r.t 1)
  • N(s, 4) = 2 (out of place w.r.t 3, 1)
  • N(s, 5) = 2 [out of place w.r.t. 3, 1]
  • N(s, 6) = 2 [out of place w.r.t. 3, 1]
  • N(s, 8) = 2 [out of place w.r.t. 3, 1]
  • N(s, 3) = 1 [out of place w.r.t. 1]
  • N(s, 1) = 0 [no tiles out of place]

• N(s) = $6+1+2+2+2+2+1+0=16 \rightarrow$ Even Parity

Implementing Parity

def num_inversions(self):
  total = 0
  for i in range(len(self.squares)):
    if self.squares[i] == '_':
      continue
    si = int(self.squares[i])
    for j in range(i, len(self.squares)):
      if self.squares[j] == '_':
        continue
      sj = int(self.squares[j])
      if si > sj:
        total += 1
  return total

def get_parity(self):
  return self.num_inversions() % 2

# In the main solution code, we write
if p1.get_parity() != p2.get_parity():
		print('No solution')
		return

Exercise 2.4: Actions with Costs

cost = {'up':1, 'down':2, 'left':3, 'right':4}

• UCS will find a solution which is optimum in terms of cost, as all actions have non-negative cost
• When the weight of all edges is equal (e.g. all have cost == 1), then UCS will expand nodes in the same order as BFS (producing the same solution)