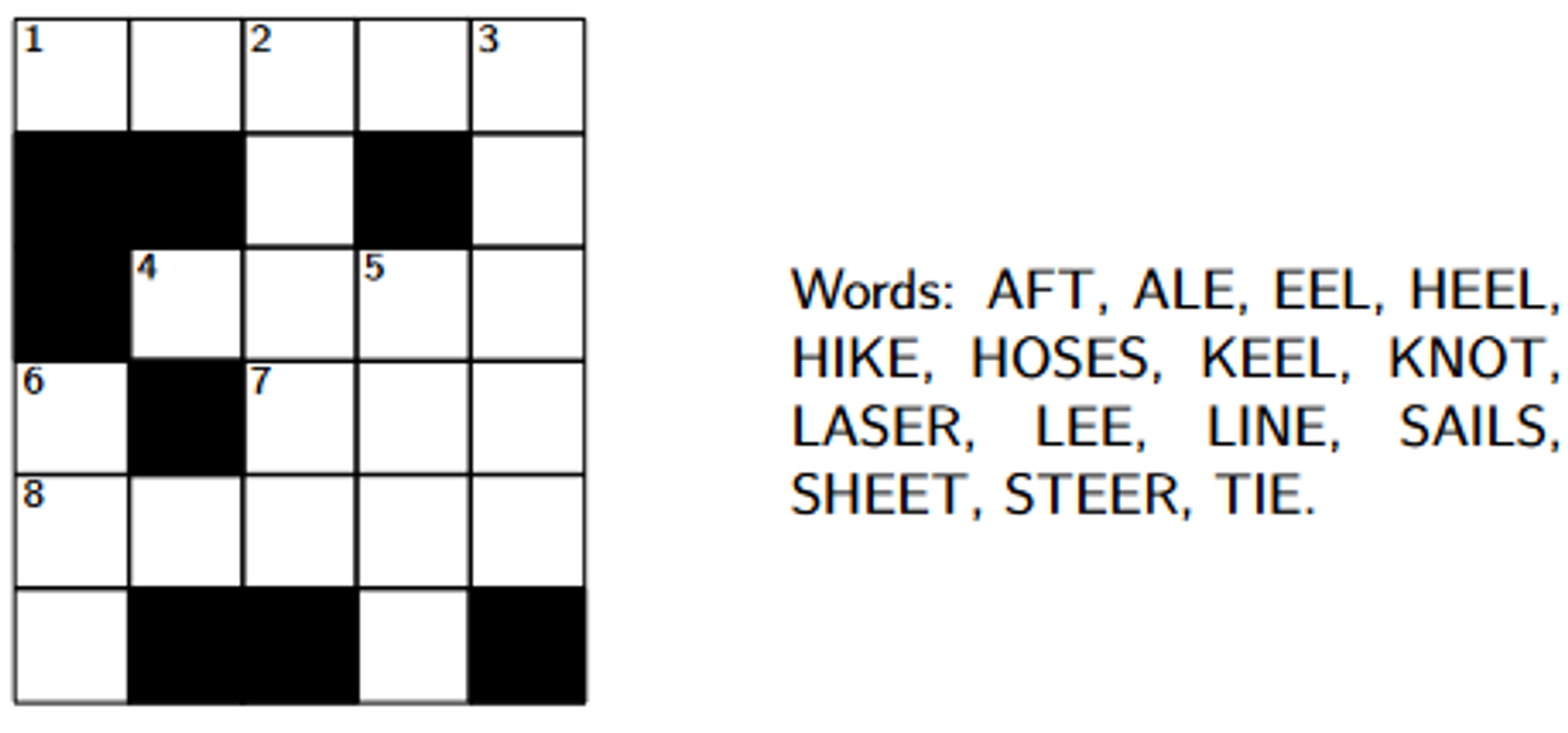
Exercise 4.1 - Crossword Puzzle

Exercise 4.1 - Crossword Puzzle; Variables, Domains and Constraints

1. List the variables and their domains in the CSP representation of this crossword puzzle
2. List the constraints in the CSP representation of this crossword puzzle.

Exercise 4.1a - Variables and their Domains

Variables are the fields that we are trying to assign a value to (in this case, they are an array of characters). In this case, the variables that we can assign values to are 1-across, 2-down, 3-down, 4-across, 5-down, 6-down, 7-across-, 8-across.

Domains are the set of values which each variable can hold (that is, the complete set of values that can be assigned to any variable). In this case, the domains are {ALE, EEL, HEEL, HIKE, HOSES, KEEL, KNOT, LASER, LEE, LINE, SAILS, SHEET, STEER, TIE}

Exercise 4.1b - Constraints in the CSP representation

Domain Constraints are constraints that are applied to each variable in isolation. For this crossword, an example of a domain constraint is that variables can be set to only the words of the correct length.

Binary Constraints on the other hand are constraints that apply to two variables at a time. For this crossword example, a binary constraint would be that the letter at an intersection point must be the same for both words.

Global Constraints are constraints that apply to all variables. In this case, each word can only be used once.

We want to use constraints to help us prune down the domains (the possible values for each variable) and thus reduce the complexity of the problem.

Domain Constraints: The set of words are constrained to {ALE, EEL, HEEL, HIKE, HOSES, KEEL, KNOT, LASER, LEE, LINE, SAILS, SHEET, STEER, TIE}

Binary Constraints: The words at each intersection must be the same:

• 1A[2]=2D[0] (The value at index 2 of variable 1A must be the same as the value at index 0 of 2D

Exercise 4.2 - Constraint Violations

1. Start to sketch a constraint graph for the crossword CSP. Choose one variable, then sketch out the constraints that the variable occurs in, and finally include any other variables that are also in scope of the constraints you have already drawn. The full constraint graph will be too large to draw easily.
2. Apply domain consistency to this CSP, and re-state any variable domains that change. Does the structure of the constraint graph change?

Exercise 4.2a

Bipartite have a few key features for denoting constraints

• Circular or Oval-Shaped Nodes representing each variable
• Rectangular nodes for each constraint
• Domain of values associated with each variable
• An Arc (Line) from variable X to each constraint that involves X

• Constraint graphs are another way of visualise constraints
• Each line represents a single constraint
• Also represent length as other 'variables' to enforce the constraints
• Double arrow means that if one is affected, the other is affected.

Exercise 4.2b - Domain Consistency

In applying domain consistency, domains are reduced to those with answers with word lengths that are consistent with the number of blank spaces in the variable, so all variable domains are changed.

• Remove all entries that don't match the length constraint
• $dom[1A] =\{\text{HOSES, LASER, SAILS, SHEET, STEER}\}$
• $dom[2D] =\{\text{HOSES, LASER, SAILS, SHEET, STEER}\}$
• $dom[3D] =\{\text{HOSES, LASER, SAILS, SHEET, STEER}\}$
• $dom[4A] =\{\text{HEEL, HIKE, KEEL, KNOT, LINE}\}$
• $dom[5D] =\{\text{HEEL, HIKE, KEEL, KNOT, LINE}\}$
• $dom[6D] =\{\text{AFT, ALE, EEL, LEE, TIE}\}$
• $dom[7A] =\{\text{AFT, ALE, EEL, LEE, TIE}\}$
• $dom[8A] =\{\text{HOSES, LASER, SAILS, SHEET, STEER}\}$
• We're not worried about letter intersections / duplicated words at this stage
• If the nodes have the same structure then we will have a graph with the same structure.
  • The constraint graph does not change in structure.

At this point, we are not concerned about the constraints on letter intersections or word duplicates; That will come later.

Exercise 4.3 - Backtracking Search

Apply backtracking search to the node-consistent constraint graph. Record the number of nodes expanded in the search procedure. You can trace the algorithm manually (e.g. sketching a search a tree) or develop code to answer this question.

• We want to systematically explore the domain by instantiating variables one at a time
• Evaluate each constraint predicate as soon as all of its variables are bound.
• Any partial assignment that doesn't satisfy the constraint can be pruned from the domain (of that variable)
• This is essentially "brute forcing" our way to a solution

• To solve the CSP, we need to know the variables, domains and constraints.
• Backtracking search can be manually traced or implemented by following the pseudocode given, in which backtracking search is implemented recursively.

• We could convert the recursive implementation into an iterative implementation by 'unrolling' it.

select unassigned variable (i.e. no word attached)
for each possible value in the domain for that variable:
		for constraint in constraints:
				if constraint is not violated:
						variable <- value
						# also update vlaue in the assignment dictionary
						# call next level of recursive backtracking.

Backtracing Search - Manual Solution

1. Select $\text{1-Across}$ as the first unassigned variable?
2. Does the value $\text{HOSES}$ violate any constraints? No! So let's expand search from this node.
   • Consistent with the rules, so expand this node's children
3. Using the recursive function call, select $\text{2-Down}$ as the next unassigned variable.
4. Does the first $\text{HOSES}$ violate any constraints? Yes - we can't re-use words! Let's try the next variable.
5. Does the second value $\text{LASER}$ violate any constraints? Yes - {HOSES[3] ≠ LASER[0]}
6. Does the third value $\text{SAILS}$ violate any constraints? No! So expand search from node.
   • Consistent with the rules, so expand this node's children
7. Using the recursive function call, select $\text{3-Down}$ as the next unassigned value
8. $\cdots$ continue until assignment for all variables found that doesn't violate any constraints

Backtracking Search - Code Solution

• Implemented recursively.
• The maximum recursive depth is determined by the number of variables
• If there are more than 100 variables, convert the backtracking search from the recursive to iterative solution by unrolling it to prevent a stack overflow exception

Code Solution - Environment (Crossword) Class

class CrossWord:
  def __init__(self):
    self.constraint_checks = 0
    self.words = { # Set of possible variable allocations
        "AFT", "ALE", "EEL", "HEEL",
        "HIKE", "HOSES", "KEEL", "KNOT",
        "LASER", "LEE", "LINE", "SAILS",
        "SHEET", "STEER", "TIE"
    }

    self.vars = { # Variables and their current assignments;
				# a map of variable names -> variable assignments (assignment from self.words)
        "1A": "", "2D": "", "3D": "", "4A": "",
        "5D": "", "6D": "", "7A": "", "8A": ""
    }


    self.length_constraints = {
        "1A": 5, "2D": 5, "3D": 5, "4A": 4,
        "5D": 4, "6D": 3, "7A": 3, "8A": 5
    }

    self.intersect_constraints = {
        "1A": [("1A", 2, "2D", 0), ("1A", 4, "3D", 0)],
        "2D": [("2D", 0, "1A", 2), ("2D", 2, "4A", 1),
               ("2D", 3, "7A", 0), ("2D", 4, "8A", 2)],
        "3D": [("3D", 0, "1A", 4), ("3D", 2, "4A", 3),
               ("3D", 3, "7A", 2), ("3D", 4, "8A", 4)],
        "4A": [("4A", 1, "2D", 2), ("4A", 2, "5D", 0), ("4A", 3, "3D", 2)],
        "5D": [("5D", 0, "4A", 2), ("5D", 1, "7A", 1), ("5D", 2, "8A", 3)],
        "6D": [("6D", 1, "8A", 0)],
        "7A": [("7A", 0, "2D", 3), ("7A", 1, "5D", 1), ("7A", 2, "3D", 3)],
        "8A": [("8A", 0, "6D", 1), ("8A", 2, "2D", 4),
               ("8A", 3, "5D", 2), ("8A", 4, "3D", 4)]
    }

    self.domains = {
        k: [word for word in self.words if len(word) == self.length_constraints[k]]
        for k, v in self.vars.items()
    }

Code Solution - Backtracking Algorithm

def recursive_backtracking(env, assignment, expanded=0, verbose=False):
    # Locate an empty assignment
    unassigned = None
    for key, val in assignment.items():
        if val == "": # The variable hasn't been assigned;
            unassigned = key
            break

    if unassigned is None: # All variables have been assigned
        return assignment, expanded

    for word in env.domains[unassigned]:
        # Select a potential assignment
        assignment[unassigned] = word

        # Check assignments validity
        if not env.check_constraints(assignment):
						# Find another assignment;
            continue

        # lock in current value and expand other nodes
        result, expanded = recursive_backtracking(env, {k: v for k, v in assignment.items()}, expanded + 1)
        if result is not None:
            if verbose:
                print("Number of backtracks", expanded)
            return result, expanded

    return None, expanded
===================================================================
env: crossword class / state
assignment: var name -> word
expanded: counter of number of nodes expanded (measure of performance)

Exercise 4.4 - Arc Consistency

• The simplest form of constraint propagation, which repeatedly enforces local constraints

• An arc $\langle x, r(X,\bar{y})\rangle$ is arc consistent for every value $x \in \text{dom}(X)$ there is some value $\bar y\in\text{dom}(\bar{Y})$ such that the constraint $r(x,\bar y)$ is satisfied.

• An $\langle x, r(X,\bar{y})\rangle$ is consistent if, for every single value $x\in X$there is some allowed $y$. We want to prune (reduce) the domains using the arc consistency algorithm

1. Begin with 𝑑𝑜𝑚_1𝐴={𝐻𝑂𝑆𝐸𝑆, 𝐿𝐴𝑆𝐸𝑅, 𝑆𝐴𝐼𝐿𝑆, 𝑆𝐻𝐸𝐸𝑇, 𝑆𝑇𝐸𝐸𝑅}
   • Check for a value in 𝑑𝑜𝑚_2𝐷 consistent with each element of 𝑑𝑜𝑚_1𝐴
   • We have the constraint that 1𝐴[2]==2𝐷[0]
   • Remove {𝑆𝐴𝐼𝐿𝑆, 𝑆𝐻𝐸𝐸𝑇, 𝑆𝑇𝐸𝐸𝑅} from 𝑑𝑜𝑚_1𝐴 as they violate arc-consistency (are not consistent)
   • That is, set 𝑑𝑜𝑚_1𝐴={𝐻𝑂𝑆𝐸𝑆, 𝐿𝐴𝑆𝐸𝑅}
   • Continue with checking – check for a value in 𝑑𝑜𝑚_3𝐷 that is consistent with each element in 𝑑𝑜𝑚_1𝐴
   • Remove {𝐿𝐴𝑆𝐸𝑅} as it is not arc consistent.
   • Therefore, 𝑑𝑜𝑚_1𝐴={𝐻𝑂𝑆𝐸𝑆} as the other values are not arc consistent.

Code Solution

Arc Consistency Algorithm

def arc_consistency(env, verbose=False):
    constraint_checks = 0
    domains = {
        k: [word for word in env.words if len(word) == env.length_constraints[k]]
        for k, v in env.vars.items()
    }   
    container = [x for k, v in env.intersect_constraints.items() for x in v]
    while container != []:
        constraint_checks += 1
        n1, i1, n2, i2  = container.pop(0)         # Revise the CSP
        prior_len = len(domains[n1])
        avail_letters1 = set(word[i1] for word in domains[n1])
        avail_letters2 = set(word[i2] for word in domains[n2])
        result = avail_letters1.intersection(avail_letters2)
        # Update the domain based on the revision
        domains[n1] = [word for word in domains[n1] if word[i1] in result]
        if domains[n1] == []:  # No solution exists
            return None
        elif len(domains[n1]) != prior_len:
            # If domain changes, reconsider constraints for neighbouring nodes
            for n, i, m, j in env.intersect_constraints[n1]:
                if m != n2:
                    # We shedule neighbour m to be updated with 
                    # the new domain of n (our current node)
                    container.append((m, j, n, i))  
   
    if verbose:
        print(f"Number of arc constraint checks: {constraint_checks}")  
       
    return domains

Performance Testing Code

env = CrossWord()

recursive_backtracking(env, {k: v for k, v in env.vars.items()}, verbose=True)
arc_consistency(env, verbose=True)

print("Number of backtracking constraint checks", env.constraint_checks)

import time
samples = 1000
env = CrossWord()
start = time.time()
for i in range(samples):
    recursive_backtracking(env, {k: v for k, v in env.vars.items()})
print("backtracking", (time.time() - start) / samples)
start = time.time()
for i in range(samples):
    arc_consistency(env)

print("arc", (time.time() - start) / samples)

• When comparing the performance of the backtracking algorithm vs the arc consistency algorithm, we get the following results:

• Number of backtracks: 37

• Number of arc-constraint checks: 54

• Number of backtracking constraint checks: 167

• Backtracking: 0.0005723941326141358 s

• Arc: 0.00013731718063354493 s

• Continue repeating this process – if you apply arc consistency correctly, it should solve the crossword puzzle.
• Even allowing for different variations of counting the number of operations, the AC-3 algorithm still solves the problems in many fewer operations than backtracking search