1.0 - Dynamic Programming

A dynamic programming solution might apply to an optimisation problem with:
- Optimal substructure, e.g. the longest common subsequence problem, and
- Overlapping subproblems
Dynamic programming solutions solve a problem by
- Solving all sub-problems (once each) and,
- Using those solutions to choose the sub-problem that will give the optimal answer.

2.0 - Greedy Problems

A greedy algorithm may be found for optimisation problems with

Optimal sub-structure and
The greedy choice property

Greedy problems solve problems by making a greedy choice (locally optimal choice) and solving (only) the chosen sub-problem

If applicable, prefer these to dynamic programming problem since we have fewer sub-problems to solve.

2.1 - Greedy Choice Property

Some optimisation problems with optimal substructure have the greedy-choice property:
- Given a problem, we know which sub-problem will yield an optimal solution without having to calculate the solutions to all of the sub-problems it depends on (meaning that we don’t have to compute all sub-problems)
- To solve a problem, we can make a greedy choice (a locally optimal choice) about which sub-problem to solve, and then just solve that one
If a problem has the greedy choice property, then locally optimal choices lead to globally optimal solutions

2.2 - Greedy Algorithms

🌱 Here are some of the Greedy Algorithms that we have already seen:

Prim’s Minimum Spanning Tree Algorithm
- The minimum spanning tree of a weighted graph G, that is a superset of tree T (a connected acyclic sub-graph of G) is either:
  - Base case: T if the tree is already spanning
  - Recursive case: $T\cup\{(u,v)\}$ where $(u, v)$ is the least weight edge leaving T
Kruskal’s Minimum Spanning Tree Algorithm
- The minimum spanning tree of a weighted graph G, that is a superset of a forest of trees T (a spanning acyclic sub-graph of G) is either:
  - Base case: T if it is already connected
  - Recursive case: $T\cup\{(u, v)\}$ is the least weight edge connecting any two trees in the forest T
Dijkstra’s Single-Source Shortest Path Algorithm
- The shortest path tree of a weighted graph G from a source vertex s that is a superset of a shortest-path tree from T from s to $G.V-Q$ $G . V - Q$ of the vertices in G is either:
  - Base case: $T$ , if $Q$ is empty
  - Recursive case: $T\cup \{(u, v)\}$ where $(u, v)$ is the edge connecting vertex $u\in T$ to the vertex $v\in Q$ that is the closest to $s$ (has the highest priority in $Q$ )

2.3 - Activity Selection Problem

🌱 Find the combination (subset) of tasks that maximises the number of activities in a finite amount of time:

Given:
- A list of tasks, $t_1, \cdots, t_n$
- And their start and finishing times $s_1, \cdots, s_n$ and $f_1, \cdots, f_n$
Which subset of tasks maximises the number of activities?
- Each of the tasks are represented as a pair of start and finishing times
Greedy Strategy: Always pick the compatible activity (no overlap) that finishes first.
We first want to sort the activities on finishing times - for $n$ activities, this takes $\Theta(n\lg n)$ time
Accumulate compatible activities in a set, $A$ , initialised to contain the fisrt activity
Pick the next activity that starts after the latest finish time so far $k$

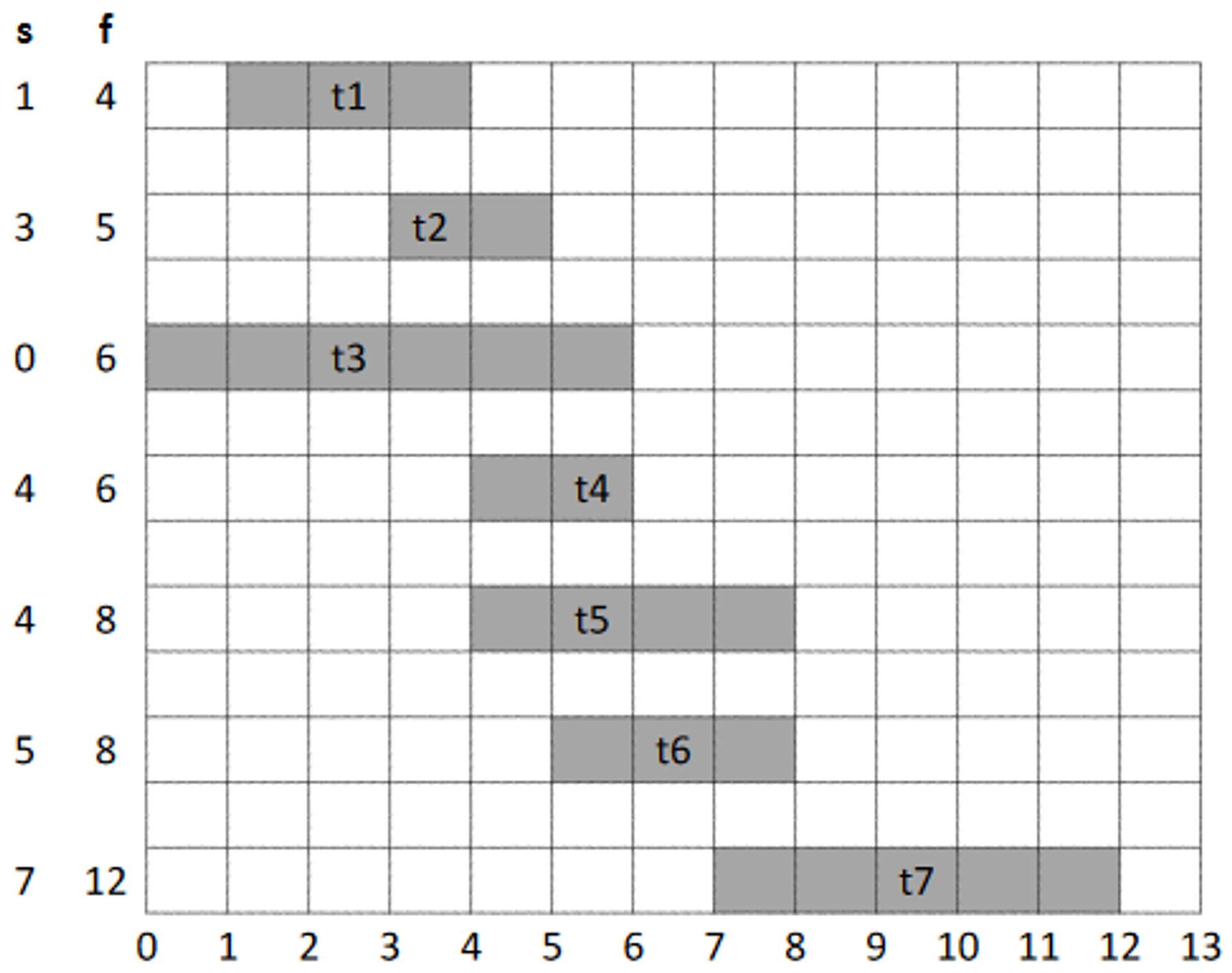
The loop is $\Theta(n)$ , so the dominant factor is the sorting $\Theta(n \lg n)$

Greedy-Activity-Selector(s, f)
    n = s.length
    A = { a1 } // The activity that finishes first
    k = 1
    for m = 2 to n
        if s[m] >= f[k]
            A = A u { am }
            k = m
    return A

In this example from above, we choose $t_1$ $t_{1}$ first as it has the earliest finishing time - this gives the most time for all other tasks - we need to choose tasks that start at earliest $t=4$ $t = 4$
- Then, $t_2$ cannot be chosen since it’s starting time is before $t_1$ ’s finishing time.
- Likewise, we cannot choose $t_3$
However, we can choose $t_4$ $t_{4}$ , as it’s starting time is equal to the finishing time of $t_1$ $t_{1}$ - we now need to choose tasks that start at earliest $t=6$ $t = 6$
- Then, $t_5$ cannot be chosen as it’s starting time is $4$ , and it overlaps with $t_4$ .
- Likewise, we cannot choose $t_6$
We can choose $t_7$ .

Proof

Suppose your algorithm generates the optimal set of tasks $a_1, a_2, a_3, \cdots, a_n$
Prove that the set $b_1, b_2, b_3\cdots, b_{m}$ doesn’t exist
Suppose that the sequences above are sorted by finishing time.
Additionally, suppose that $a_1=b_1, a_2=b_2, a_3=b_3$ and $a_4\ne b_4$ (that is, $a_4\ne b_4$ is the first time the sequences differ.)
Let’s argue that we could replace $b_4$ in the sequence $b_1, b_2, \cdots , b_{n+1}$ by $a_4$
- Since $a_4$ is compatible with activities $a_1, a_2, a_3$ and $a_1=b_1, \cdots a_3=b_3$ then $a_4$ is compatible with $b_1, b_2, b_3$
- Additionally, since the finishing times are compatible, we have that $a_4$ is compatible with $b_5, \cdots$
By the same argument, we can replace $a_5$ by $b_5$ .
If the sequence $b_1, b_2, \cdots, b_m$ is longer, then we have a contradiction, as we have already found that a shorter sequence is optimal (and thus this $b$ sequence is not optimal)
Otherwise, if they’re of equal length, then they are the same sequence

2.4 - Knapsack

Consider a set of items, each with a value $v$ , and weight $w$ .
What is the maximum value you can fit into a knapsack, holding a maximum total weight of $w$ $w$ ?
- Problem 1 - Fractional Knapsack
  - You may take part amounts (fractions) of items
  - Greedy strategy: Take as much as possible of the item that maximises $\frac{v}{w}$
  - This is optimal, and can be solved using the greedy approach.
- Problem 2 - Binary Knapsack
  - You must take all or none of each item
  - Greedy strategy: Take all of the item that maximises $\frac{v}{w}$
  - This is not optimal

2.4.1 - Fractional Knapsack

Consider a case where we have three items and a knapsack with 50 units of space.
From the asribed values and weights, we can compute the value $\frac{v}{w}$ $\frac{v}{w}$ of each item
- Item 1: $\frac{60}{10}=6.0$
- Item 2: $\frac{100}{20}=5.0$
- Item 3: $\frac{120}{30}=4.0$

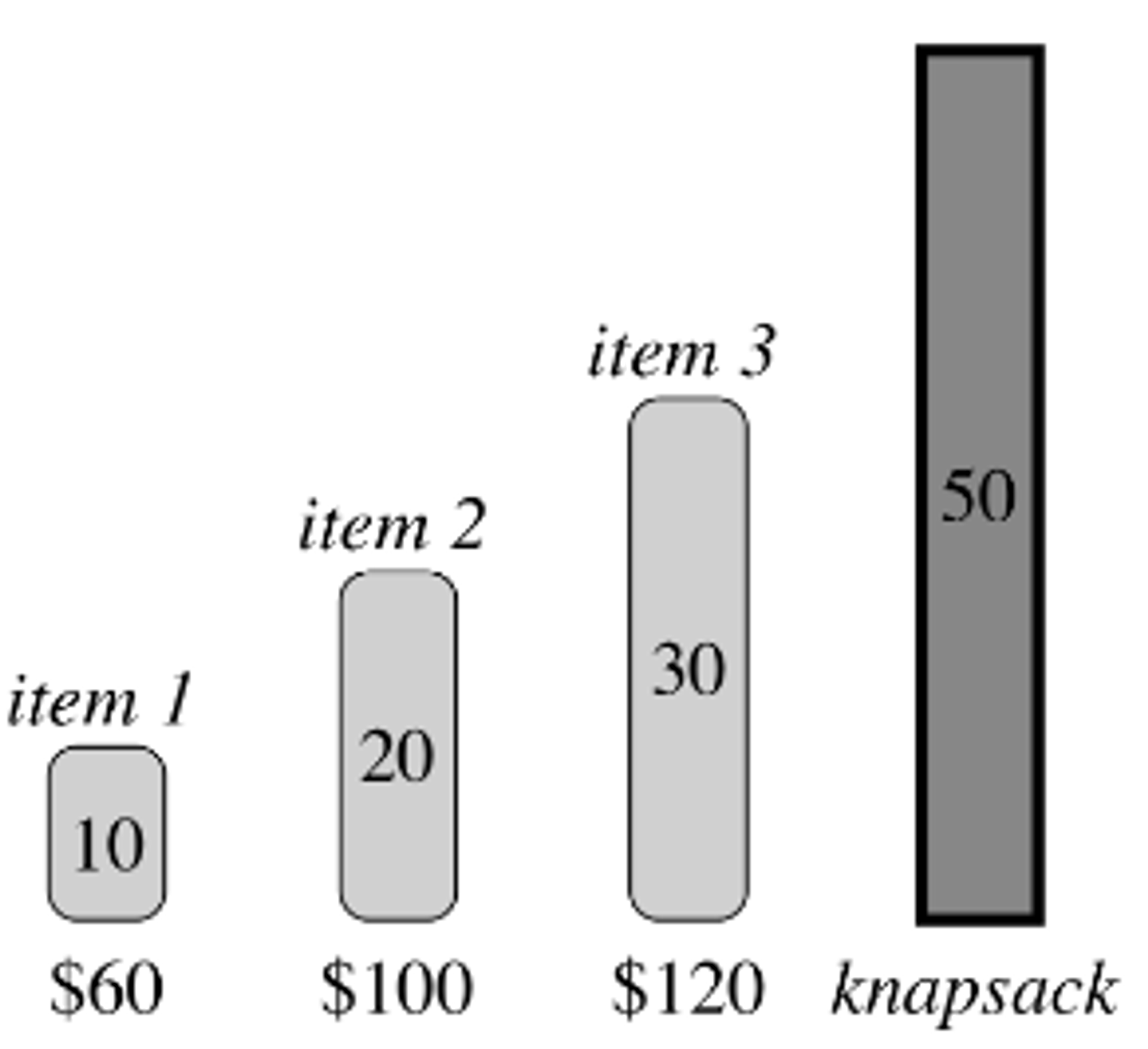
The greedy strategy works for the fractional case, in which you start with the item with the most value per weight.
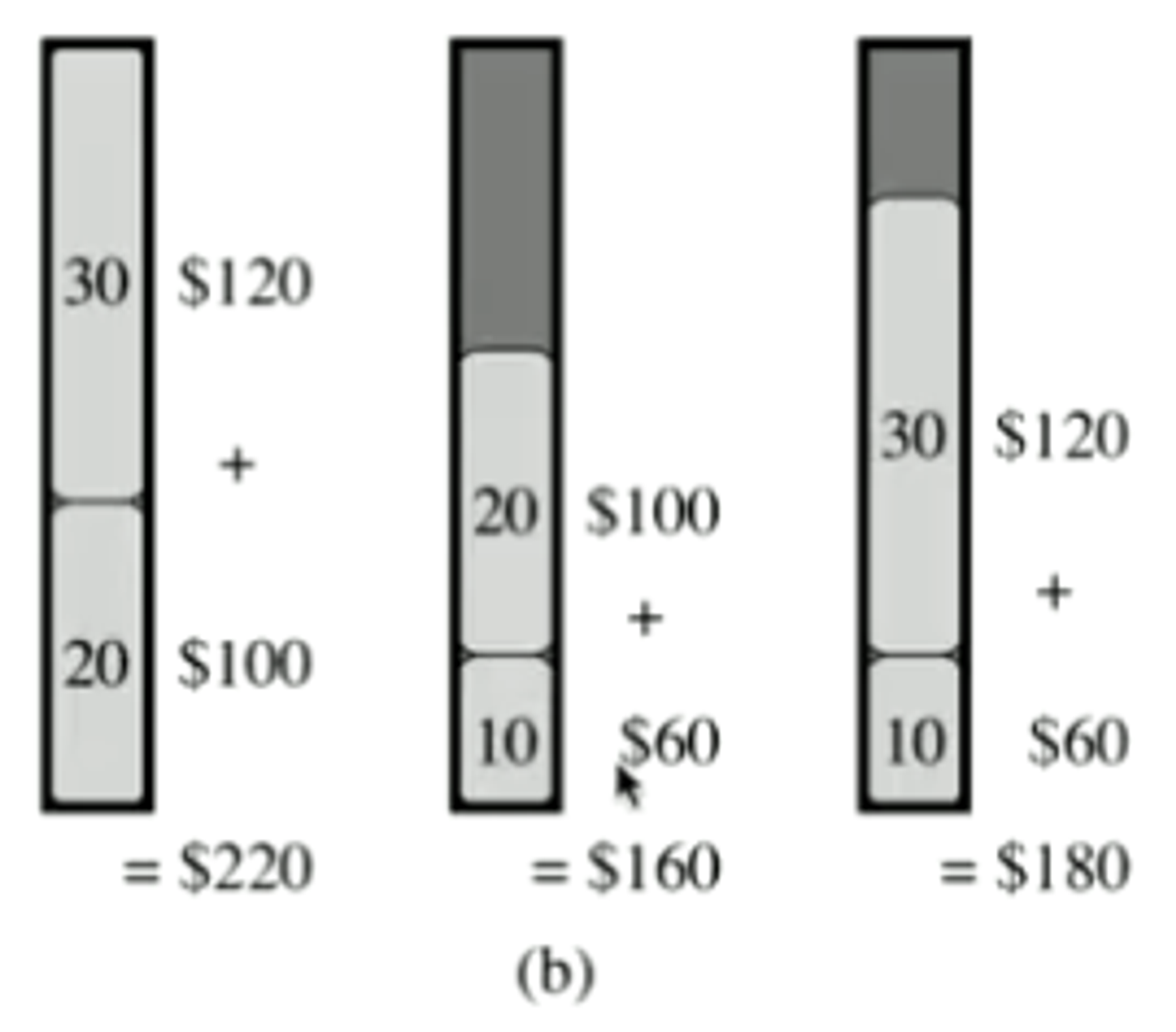
However, this doesn’t work for the binary case:
- Consider in the binary case using the greedy strategy.
- We’d first choose Item 1 and then item 2, leaving 20 units of space unoccupied (value of $160)
- However, the optimal strategy is to take item 2 and item 3 (value of $220)

2.4.2 - Binary Knapsack

Let there be $n$ items, $\def\it{\text{item}}\it_1, \it_2, \it_3, \cdots, \it_n$ where:
- The value of the $i^{\text{th}}$ item is $\text{value}[i]$
- The weight of the $i^{\text{th}}$ item is $\text{weight}[i]$
Define the recurrence:

$\text{BinaryKnapsack}(i, w)\ \ \ \ \ \ \ \ \text{where}\ \ \ \ \ \ \ 0\le i\le n$

To be the maximum value of the items, $\def\it{\text{item}}\it_1, \it_2, \it_3, \cdots, \it_n$ that can fit into a knapsack of size $w$