1.0 - Amortised Analysis

• So far, we have analysed algorithms for “one-off” use.

• However, we often used a data structure (object) for a purpose that involves many uses of its methods

  • For example, the multiple calls to extract-min from a priority queue.

  Dijkstra(G, w, s)
  	// (G) Graph, (w) weight function, (s) source vertex
  	init_single_source(G, s)
  	S = ∅         // S is the set of visited vertices
  	Q = G.V       // Q is a priority queue, maintaining G.V - S
  
    while Q != ∅
  			u = extract_min(Q)
  			S = S ∪ {u}
        for each vertex in G.adj[u]
            relax(u, v, w)
  

• We want to determine the worst-case time complexity of a series of operations, rather than just a single operation in isolation

• Consider an object x with multiple operations

  • The “worse” is worst-case $O(n)$
  • You design an algorithm that uses object x’s method $n$ times
  • Naively, the worst-case time complexity is $O(n^2)$

• However, you may know that the worst-case cannot happen $n$ times in a row - in this case, how can you prove that the implementation is actually better then $\Theta(n^2)$

• Amortised analysis considered sequences of operations, typically that successfully modify a data structure

1.1 - Dynamic Table Example

Store an initially unknown number of elements in an array.

• Double the size of the array when it runs out of space

Typically, inserting an element into an array is constant time

• However, sometimes one must:
  • Allocate a new, larger array (of twice the size)
  • Copy all of the elements to the new array, and add the new element.

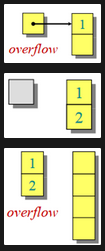
Suppose our array initially has size 1.

1. Inserting the first element into the array succeeds.

2. Inserting the second element into the array fails, so we must construct a new array, copy over the old elements + new element.

3. Following this, the insertion of the third element once again causes the array to over flow, and thus we must construct a new array, copying over the new elements.

• After $n$ operations (of inserting a new elements) there are $n$ elements in the array

• Inserting an element when the capacity is full (worst case $n=2^i$ for some $i$) is $\Theta(n)$

• Thus, inserting $n$ elements is $\Theta(n^2)$?

  • No, it is still $\Theta(n)$

• We are analysing:

  for 1 = 1..n
      insert(e_i)
  

• for some sequence of elements $e_1, e_2, \cdots, e_n$

• The vast majority of insertions are constant time

• How many are not, and what their cost are depend on $i$

1.1.1 - Tighter Analysis on Dynamic Table

Let $\begin{aligned} c_1=&\ \text{the cost of the ith insertion}\\ =&\begin{cases}i\ \ \ \ &\text{if } {i-1}\text{ is an exact power of 2}\\ 1&\text{otherwise}\end{cases} \end{aligned}$

From this, we get:

• Inserting the 1st, 4th, 6th, 7th, 8th, 10th element takes constant time as we have space
• Inserting the 2nd element has a relative cost of 2:
  • Copy across existing element
  • Copy across new element
• Inserting the 3rd element has a relative cost of 3:
  • Copy across existing 2 elements
  • Copy across new elements

1.1.2 - Dynamic Table: Aggregate Method

🌱 Develop a summation, and solve it for $n$ operations. Develop bound for that series of operations.

• Inserting the 2nd, 3rd, 5th, 9th, … elements (when the array has size 1, 2, 4, 8, …) has an additional cost equal to the size of the array

• In general, how many resizes are there in a sequence of $n$ insert operations, for $n\ge 1$?

  $$\lceil \lg n\rceil$$

• How much does the $j^\text{th}$ resize operation cost?

  $$2^{j-1}$$

• The cost of $n$ insertions is:

  $$\begin{aligned} &\sum^n_{i=1} c_i\\ \le&\ {\color{lightblue}n} + {\color{lightgreen}\sum^{\lceil \lg n\rceil}_{j=1} 2^{j-1}}\\ \le &\ 3n\\ =&\ \Theta(n) \end{aligned}$$

  $\color{lightblue}n$ insertion operations, $\color{lightgreen}\sum^{\lceil \lg n\rceil}_{j=1} 2^{j-1}$$\color{lightgreen}$ cost from $\lceil \lg n\rceil$ resize operations, each costing $2^{j-1}$

• Thus, the average cost of each dynamic table operation is $\frac{\Theta(n)}{n}=\Theta(1)$

1.2 - Stack Operations

• Consider standard stack operations push and pop, and

  multipop(S, k) 
  		// Assumes that S is not empty, and k > 0
      while S is not empty and k > 0
          pop(S)
          k = k - 1
  

• Multipop(S, k) can be $O(n)$ (where $n$ is the size of the stack) if $k=n$

• Hence, any sequence of $n$ stack operations must be $O(n^2)$

• But can we prove a better bound?

• Yes, here’s our intuition

• Multipop will only iterate while the stack is not empty

• Each element is pushed exactly once, and popped exactly once, hence after $m$ pushes, there can be at most $m$ pops.

1.2.1 - Aggregate Method

• We want to determine the time complexity of $n$ stack operations, starting from an empty stack:

  for i = 1..n
      Push(...) or Pop(...) or Multipop(...)
  

• Arguing that these operations are $O(n)$ is clumsy using the aggregate method.

• Consider the more sophisticated techniques:

  • Accounting method - focus on the operations
  • Potential method - Focus on the data structure

1.2.2 - Accounting Method

• Begin the accounting method by calculating the actual cost $c_i$ of each operation

  • Push: 1
  • Pop: 1
  • Multipop(S, k): $k', k=\min(\text{size}(S), k)$

• Assign an amortised cost $\hat{c_i}$ to each method

  • Push: 2
  • Pop: 0
  • Multipop(S, k): 0

• For any sequence of stack operations, the amortised cost must be an upper bound on the actual cost

• Then, one can use the amortised cost in place of the (more complicated) actual cost

• In the above case, ever operation has a constant amortised cost, and hence a sequence of $n$ operations is $O(n)$

• We must show that the total amortised cost minus the total actual cost is never negative

  $$\sum_{i=1}^n \hat{c_i}\ge \sum_{i=1}^n c_i$$

  For all sequences of all possible lengths $n$

  	Actual Cost $c_i$	Amortised Cost $\hat{c_i}$
  Push	$1$	$2$
  Pop	$1$	$0$
  Multipop(S, k)	$k=\min(k,	S

• Our intuition here is that the extra credit in the push operation pays for the later pop operations

  • Have to PUSH an element for it to be Popped off later - so we encode this extra credit as part of the PUSH operation to be used later.

1.2.3 - Potential Method

• Focus on the data structure, instead of the operations performed on the data structure.

• Begin by determining the cost of each opeartion

• Define a potential function, $\phi$ on the data structure

• The amortised cost, $\hat{c_i}$ of an operation is the actual cost plus the change in potential

  $$\hat{c_i}=c_i+(\Phi(D_i)-\Phi(D_{i-1}))$$

• For these amortised costs to be valid, we require that the amortised cost is an upper bound on the actual cost

  • We can simplify this expression using the telescoping series.

  $$\begin{aligned} \sum_{i=1}^n \hat{c_i} &= \sum_{i=1}^n (c_i + (\Phi(D_i) - \Phi(D_{i-1})))\\ &=\sum_{i=1}^n (c_i) + \Phi(D_n)-\Phi(D_0) \end{aligned}$$

• Following on from this, the obligation is to show that $\Phi(D_i)\ge \Phi(D_0)$ after every operation (and thus $\hat{c_i}\ge c_i$)

• Consider applying the Potential method to the stack from before.
• Push and Pop both cost 1 operation
• Multipop costs $k'=\min(k, \text{sizeof}(S))$
• let $\Phi(S)$ be the size of the stack
• Our change in potential, $\Phi(D_i)-\Phi(D_{i-1})$ is modified by the size of the stack:
  • Push: 1 (the size of the stack has increased by 1)
  • Pop: -1 (The size of the stack has decreased by 1)
  • Multipop: -k’ (The size of the stack has decreased by -k’)
• From this, our amortised cost $\hat{c_i}=c_i+(\Phi(D_i)-\Phi(D_{i-1})$ is:
  • Push: 2 (1 + 1)
  • Pop: 0 (1 - 1)
  • Multipop 0 (k’ - k’)
• Our obligation is to show $\Phi(D_i)\ge\Phi(D_0)=0$ which is trivial (as the potential function gives the size of the data structure)
• Therefore, all operations have constant amortised time