1.0 - Complexity Class P

• Set of concrete decision problems that are polynomial-time solvable.

• Decision problems have a simple yes or no, $\{0,1\}$ answer

• A concrete problem is a problem whose instance set is the set of binary strings $\{0,1\}^*$

• A concrete problem is polynomial-time solvable if there exists and algorithm to solve it in $O(n^k)$ time for some constant $k$, where $n$ is the length of the binary input string

• How do we know if a concrete decision problem is in $P$?

• To show that a problem A is in P we could:

  • Come up with a polynomial-time algorithm to solve A
  • OR if we already know that another problem B is in P:
    • Find a polynomial-time reduction algorithm to transform an instance $\alpha$ of decision problem A instance to an instance $\beta$ of a decision problem B.
    • Using this, we can convert the problem instance $\alpha\rightarrow\beta$
    • We can then run algorithm B on the converted problem instance $\beta$

1.1 - Polynomial-Time Reduction Algorithm

Problem A is polynomial-time reducible to B if there exists a polynomial-time reduction algorithm to transform every instance $\alpha$ of $A$ into an instance $\beta$ of $B$

• A polynomial time reduction algorithm $F$

  • Transforms an instance $\alpha$ of a decision problem $A$ into an instance $\beta$ of a decision problem $B$
  • The transformation algorithm is polynomial time.
  • The answers are the same - if $\beta=F(\alpha)$ then $A(\alpha)=B(\beta)$
    • That is if $\alpha$ is converted to $\beta$, then $A(\alpha)=B(\beta)$

• Assuming reduce-A-to-B is a polynomial-time algorithm to reduce an instance $\alpha$ of A to an instance $\beta$ of B

• We can solve problem A in terms of B

  $\def\t{\ \ \ \ } \text{solve-A}(\alpha)\\ \t\beta=\text{reduce-A-to-B}(\alpha)\\ \t\bold{return}\ \text{solve-B}(\beta)$

• If $\text{solve-B}$ is polynomial time, and $\text{reduce-A-to-B}$ is polynomial time, then $\text{solve-A}$ is polynomial time

• Thus we have the conclusion that if B is “easy”, then so is A.

2.0 - Complexity Class NP

• The complexity class NP is the set of concrete decision problems for which a solution (a certificate) can be checked (verified) in polynomial time
  • Nondeterministic Polynomial: If you could simultaneously check all solutions to a given input, then the problem would be polynomial-time solvable
  • That is, you could non-deterministically pick the right solution and check it in polynomial time
• Problems for which we can’t even verify a solution in polynomial time are unlikely to have a polynomial time (efficient) algorithm to generate solutions

2.1 - P=NP

• Trivially, P is a subset of NP
• Are there some problems where a solution is quick to verify, but which can’t be implemented efficiently? This is unknown
• But most (everyone?) this there are, we just haven’t worked out how to prove it yet.
• This is the famous “P=NP” problem

2.2 - Example of an NP Problem - TSP

• The Travelling Salesman Problem (TSP) is to find the shortest path that visits every vertex exactly once in a graph, and returns to where it starts (assuming positive weights)
  • For the sake of reasoning, we deal with a decision problem - is there a tour of length at most $k$?
  • A solution $S$ is a list of vertices in the order visited.

check-tsp(G, S, k)
    1. Check that every vertex is in S exactly once.
    2. Check that every pair of adjacent vertices is in S is conncted by an edge in G
    3. Check that there is an edge from the last vertex to the first
    4. Sum weights of all such edges, and call the total t
    5. return t <= k

• $\text{TSP}\in \text{NP}$ is trivial to see - the above checking algorithm is in polynomial time
• We would like for it to be in $P$ - for there to be a polynomial-time algorithm that generates solutions to $\text{TSP}$
• Frustratingly, we just don’t know (yet) whether it is in $P$ or not
• This is despite
  • TSP being of practical (commercial) importance, and
  • Decades of research into efficient solutions to TSP specifically and computational complexity generally.

2.3 - Progress with P=NP (NP-Hard)

• Some progress has been made
• A concrete decision problem $B$ is $\text{NP-Hard}$ when every problem $A\in \text{NP}$ is polynomial-time reducible to $B$
• Thus, if any one of these problems can be solved by a polynomial-time algorithm then all problems in NP can be solved by a polynomial-time algorithm

2.4 - NP-Complete

• A concrete decision problem $B$ is $\text{NP-complete}$ if and only if
  • It is NP-hard and - every problem $A\in NP$ is polynomially reducible to B
  • It is in NP - solution can be verified in polynomial time
• And so, these are the hardest problems in the NP class.
• Are there any NP-complete problems? Yes!
  • It turns out TSP is in NPC
  • Thus, if you can find a way to solve TSP efficiently, you can solve a large class of important problems efficiently, and at the same time prove $P=NP$
  • In other words, you are unlikely to find an efficient solution to TSP
• That the set NPS is non-empty is a helpful clue to $P=NP$
• It seems unlikely that all problems in NP are polynomial time solvable, so “probably” the NPC problems are not polynomial-time solvable
• If you can prove that the problem you are trying to solve is NP-complete, you know that it is unlikely that it is polynomial-time solvable.

2.5 - NP Recap

• NP is the set of problems for which it is not unreasonable to think that there may be efficient solving algorithms
• We have identified a useful subset, P, for which efficient algorithms exist
• Many (theoretically and practically) important algorithms are in NP, but we don’t know whether or not they are in P
• Interestingly, we have found the subset NP-Complete, which are the “Hardest” of any in NP
• We are working towards learning a technique for showing that a problem is NP complete, then it is reasonable to stop trying to find an efficient algorithm

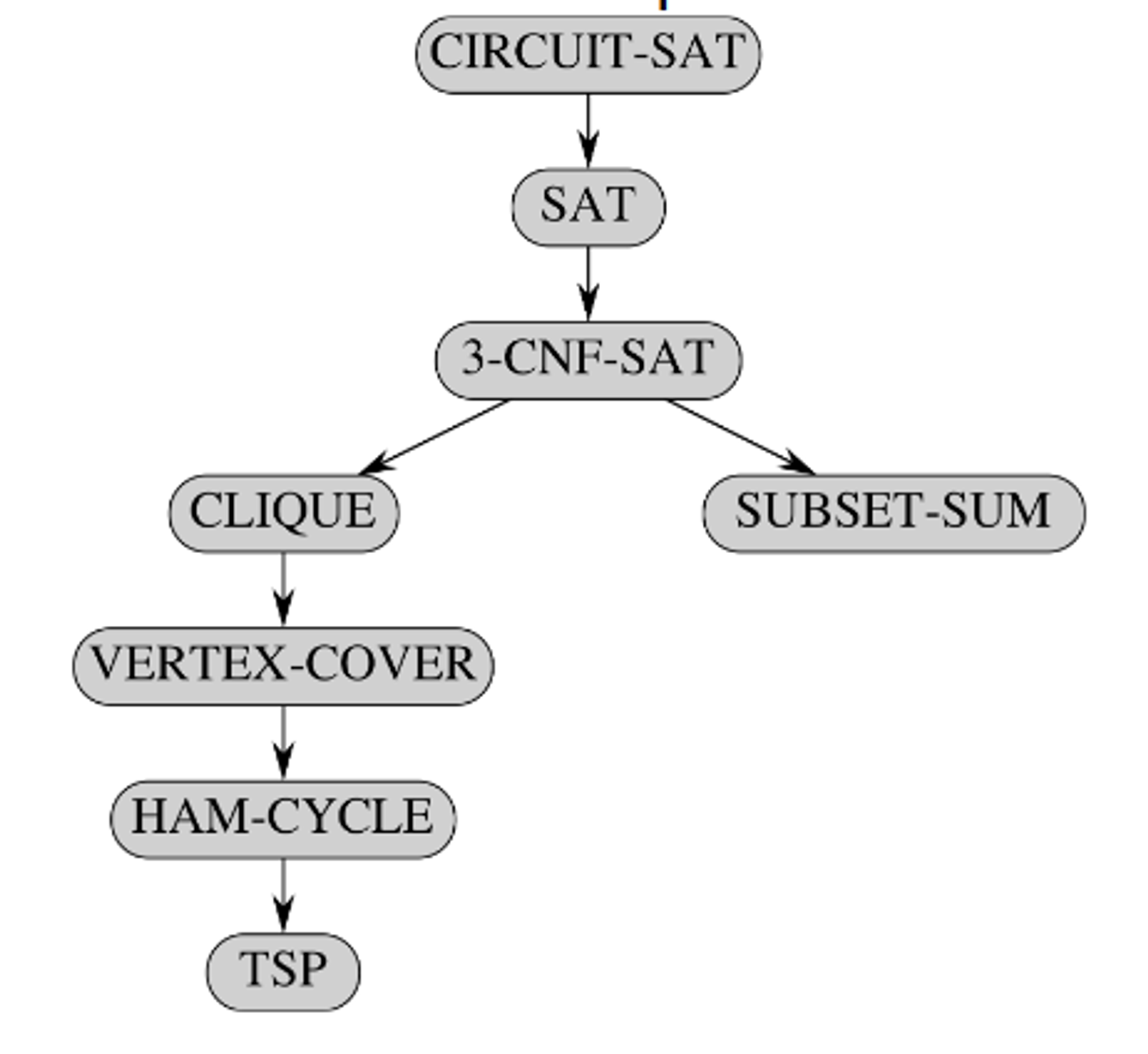
2.5.1 - NP-Complete and Cook’s Theorem

• The CIRCUIT-SAT problem is NP Complete
• This is the “first” NP complete problem
• A circuit refers to a type of logical circuit, comprised of AND and OR gates, etc.
• Cook showed that any problem in NP can be reduced in polynomial time to a circuit, that is, restated as a problem using a circuit
• Thus, if you can solve CIRCUIT-SAT in polynomial time, and your problem can be reduced to a circuit in polynomial time (any problem in NP can), then you can solve your problem in polynomial time.

2.4.2 - CircuitSAT (Circuit Satisfiability)

• A circuit is a basic concept from computer science; perform logical operations on binary inputs

• Usually consider three types of gates (NOT, AND, OR)

  

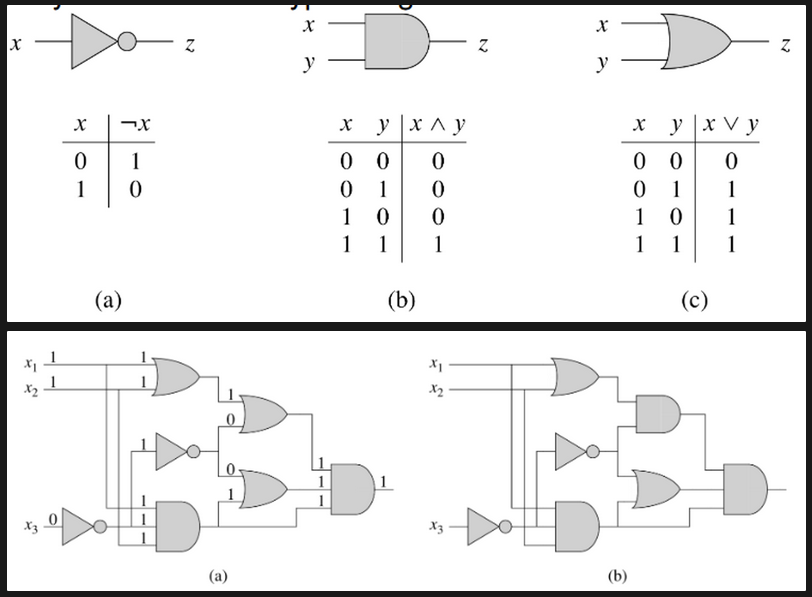
• We can compose these elements into a full circuit with no cycles and one output

• CIRCUIT-SAT asks for an assignment of 1 or 0 to each of the variables $(x_1, x_2, \cdots)$ that produces $1$ as the output

• Figure $(b)$ has no such assignment.

• Proof that CircuitSAT is NP Hard

  • All inputs may be encoded in binary format in polynomial time, and all problems can be stated as circuits
  • Thus, if CircuitSAT can be solved in polynomial time as well, other NP problems can be solved as well.

• How does Cook’s theorem help?

• Run this algorithm for solving problem $L$ with input $i$

  Solve-L(i)
      Transform (reduce) the input i to i' for CIRCUIT-SAT
      return CIRCUIT-SAT(i')
  

1. Step 1 is polynomial time and applies to all problems in NP (from Cook’s theorem)
2. Hence if Step 2 is also polynomial time, all problems in NP can be solved in polynomial time (Including those in NP-Complete)

2.6 - Reductions

💡 Using Cook’s Theorem as an intermediate to find a reduction from any NP problem to your problem - we already have a reduction from all problems to CircuitSAT, so just need to find a reduction from circuit sat to our problem.

• Let X be your own problem

• If you can show that CIRCUIT-SAT is polynomial-time reducible X, then X is NP-hard

• Why?

• If CIRCUIT-SAT reduces to X, and if you have a polynomial time solution to X, then you can solve CIRCUIT_SAT in polynomial time, and hence can then solve all NP problems in polynomial time

• That is, implement the solution to CIRCUIT-SAT as:

  CIRCUIT_SAT(i)
     Transform (reduce) the input i to i' for X
     return X(i')
  

• If you can show that CIRCUIT_SAT is polynomial-time reducible X, then X is NP-Hard

• To show that X is NP-complete, you have to show that X is in NP

  • We can show this that a solution/certificate can be verified/checked in polynomial time

• In practice, reducing CIRCUIT_SAT directly to X may be tedious.

• Instead we choose a known NP Hard problem that is closer to X

• The $\rightarrow$ operator is read as “reduces to”

• This is possible as polynomial-time reductions are transitive.

2.7 - Travelling Salesman Problem - NP Completeness

• In a weighted graph, find the least-cost path that visits every vertex once, returning to the start
• Recall the verification algorithm TSP-Check(G, S, k)
• To show that the TSP problem is in NP-Complete we need:
  • $\text{TSP}\in NP$
  • $\text{TSP}$ is in NP-Hard - to do this we need to reduce another NP-hard problem to TSP.
    • We will reduce the Hamiltonian cycle problem to the NP Hard problem

2.7.1 - TSP - Reduction from Hamiltonian Cycle to TSP

As mentioned above, we perform this step to prove that the TSP problem is NP Hard.

• A Hamiltonian cycle is a simple path through an unweighted graph that contains every vertex, starting and ending at the same vertex

• A graph is Hamiltonian if it contains a Hamiltonian cycle - this is a decision problem

  

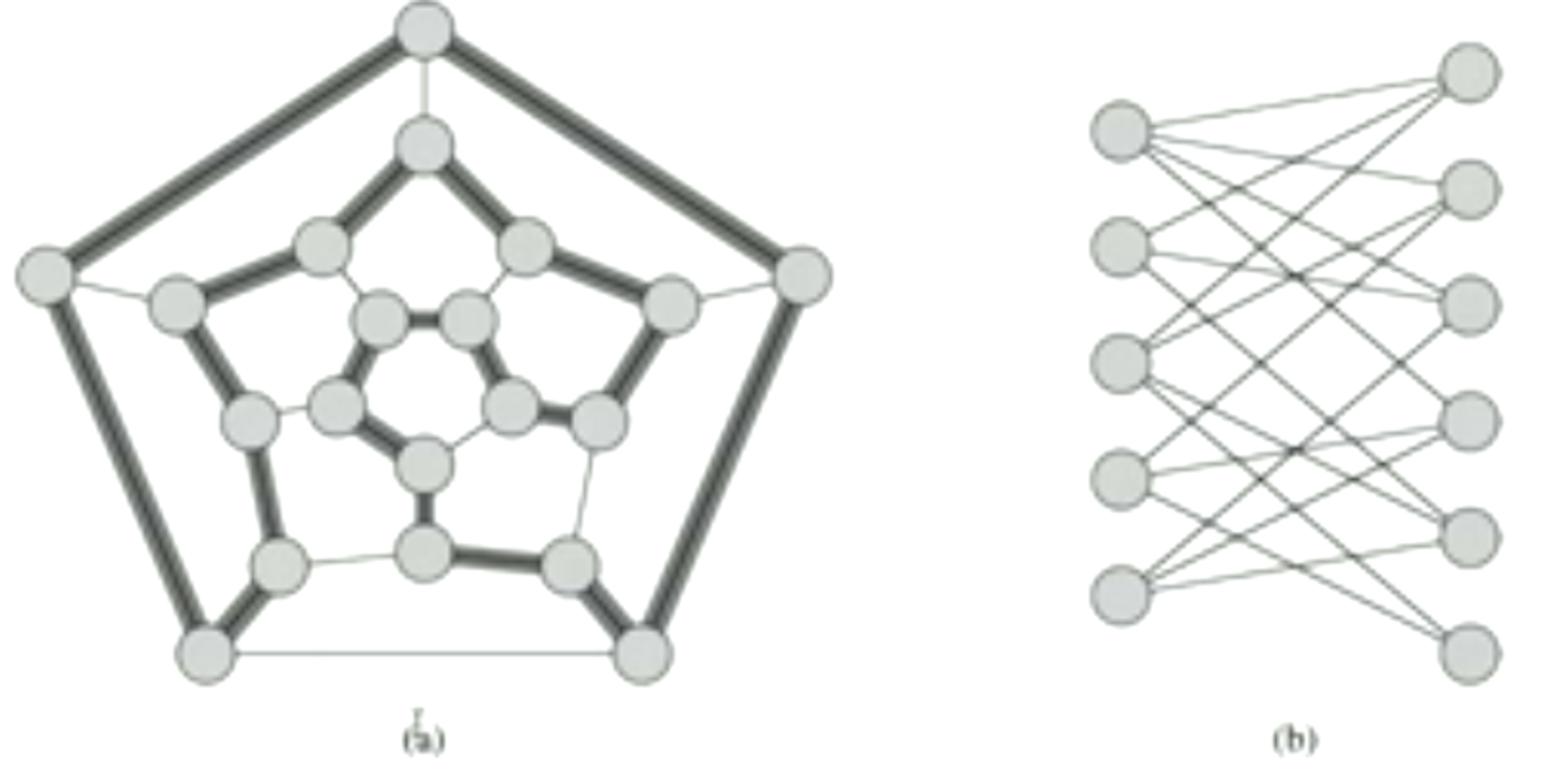
• Graph A is Hamiltonian, Graph B is not.

Recall

• Assume that we can solve TSP in polynomial time
• Then how can we use that (non-existent?) algorithm to solve HAM-CYCLE?
• We need to find a reduction from HAM-CYCLE to TSP (that is, find a way to convert the inputs from HAM-CYCLE to the inputs to TSP)
• The trick is setting the weights in the TSP version:
  • If an edge exists, give it a weight of 0
  • If not, give it a weight of 1
  • Use the TSP algorithm to find a tour with weight 0.

3.0 - Recap

• P: Polynomial time to solve

• NPC: Probably worse than polynomial-time to solve

• NP Problems that may feasibly be polynomial time (we can check a solution in polynomial time)

  $$P\subseteq NP\\ NPC\subseteq NP\\ ?? P = NP ??\\ ?? NPC \ne P ??$$

• Important first problem: CIRCUIT-SAT (recall Cook’s Theorem)

• This forms the basis of a chain of reductions, hence the set NPC is non-empty, non-singleton

• Using reduction we can show a new problem is also NPC

• Hence that problem is unlikely to have an efficient algorithm to solve it.

3.1 - Approximation Algorithms

• Many real problems have efficient algorithms that give a good approximation
• For TSP, this is enough in practice (reduce cost, not necessarily minimise cost)

💡 This algorithm, at worst is twice the cost of the optimal solution

approx-tsp-tour(G, c)
1. select a vertex r in G.V to be a root vertex
2. Compute a minimum spanning tree T for G from root r using MST-Prim(G, c, r)
3. Let L be the list of vertices visited in preorder tree walk of T
4. Return the Hamiltonian cycle H that visits the vertices in order of L

• This graph returns a tour of no more than twice the cost of an optimal tour assuming that the graph satisfies the triangle inequality:

  $$\text{For all vertices } u, v \text{ and } w \text{ in } V\\ c(u, w) \le c(u, v) + c(v,w)$$

  

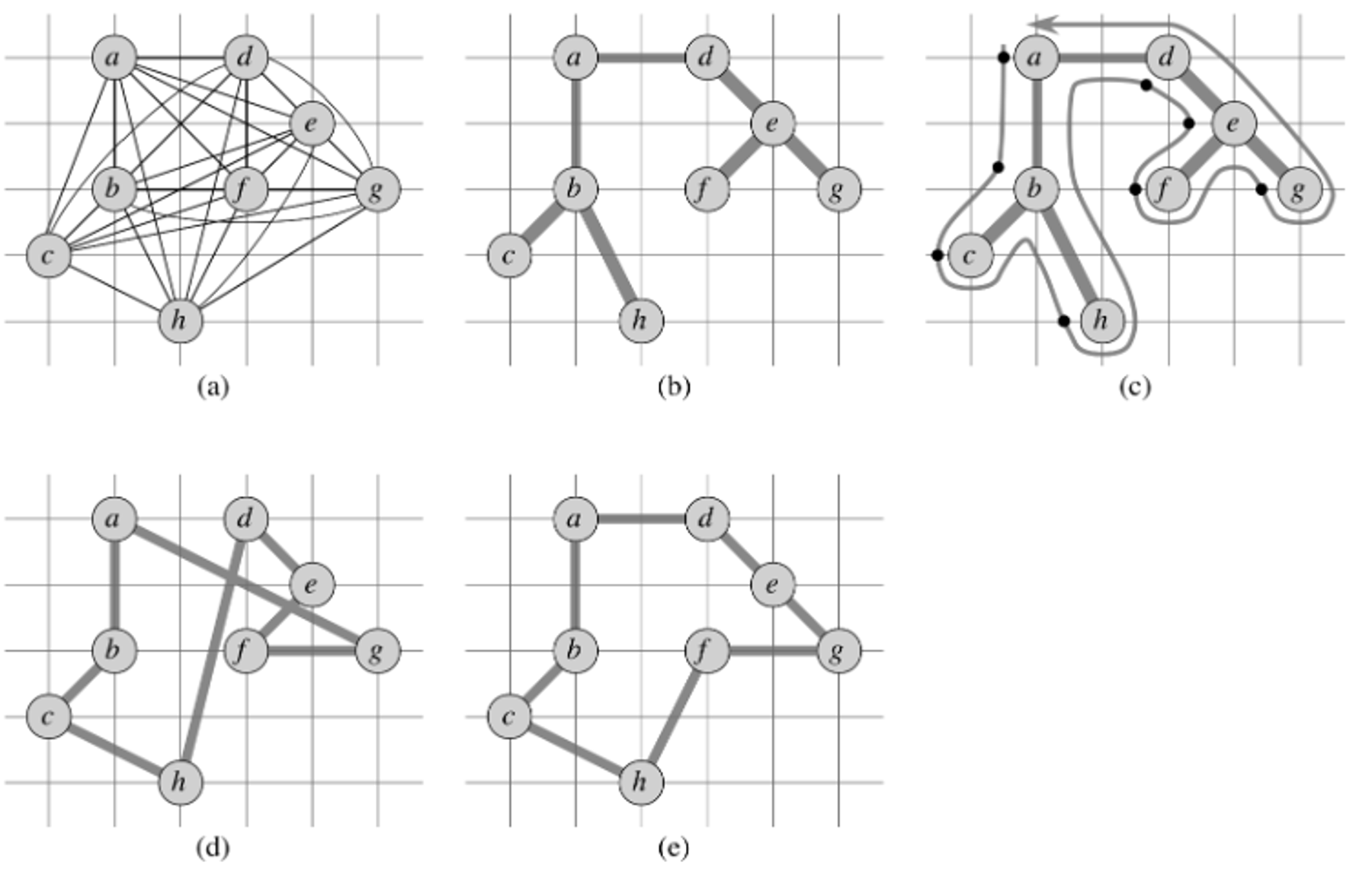
(b) is the minimum spanning tree for the graph - upper bound on the cost of the tour

(c) pre-order traversal of MST

Tour (d) is that returned by approximate-tsp-tour with cost of 19.074 - this is the tour generated by a pre-order traversal of the MST

• We avoid repeating vertices
• However, considering visiting every vertex in order via the MST traversal, we at most visit each vertex twice
• This is how we get the bound that this MST traversal is at worst twice that of the optimal solution

Tour (e) is an optimal tour, with cost 14.715

• Because of the triangle inequality, we know that the cost of going from c → h is no worse than going from c → b → h