Partition(A, p, r)
    x = A[r]
    i = p - 1
    for j = p to r - 1
        if A[j] <= x
            i = i + 1
            exchange A[i] with A[j]
    exchange A[i + 1] with A[r]
    return i + 1

1.0 - Average Case Analysis

• At the start of the semester started discussing analysis of algorithms.

• Thus far have used best and worst case analyses

  $$T_\text{worst-case}(n)=\max_{|x|=n}T(x)\\ T_\text{best-case}(n)=\max_{|x|=n} T(x)$$

• We now consider probabilistic average-case analysis

  $$T_\text{average-case}(n)=\sum_{|x|=n} T(x)\cdot Pr\{x\}$$

  • To compute this, we need to know the probability distribution of inputs of size $n$.

1.1 - Hire Assistant Example

hire_assistant(n)
    best = 0
    for j = 1 to n
        interview candidate j // at cost ci
        if candidate j is better than the best candidate
            best = j
            hire candidate j // at cost ch

Let $n:$ total number of candidates

  $m:$ number of candidates hired

Our actual cost is $n\cdot c_i+m\cdot c_h$

Our worst case is $n(c_i+c_h)$ is when $m=n$

This occurs when the candidates ordered from worst to best - they are all hired and then replaced

Our best case occurs when the candidates are ordered from best to worst

1.1.1 - Average Case Analysis

• Probability of hiring the $j$th candidate - to decide this we need to make a few assumptions

• Assume that the candidates are in random order

• Any of the first $j$ candidates is equally likely to be the best candidate.

• The probability that the $j$th candidate is the best is $\frac1j$

• Based on this probability, we can compute or average case. Thus the average cost of hiring candidates is

  $$c_h\sum_{j=1}^n \frac1j$$

• Recall the harmonic series:

  $$\sum_{j=1}^n \frac 1j=\ln n + O(1)$$

• We can randomise the input to the algorithm ourselves - this can be done for example, to reduce the probability of obtaining the worst-case time complexity of the algorithm

• Also has security implications - if attackers know that a certain algorithm runs slowly (or quickly) for a certain input, we essentially “take away” their power by randomising the input order ourselves.

1.2 - Randomised Algorithms

• An algorithm is randomised if its behaviour is determined by both:
  • Its inputs
  • Values produced by a random number generator
• For deterministic (i.e., not randomise) algorithms, we can calculate the average running time, based on a probability distribution of inputs.
• For randomised algorithms we can calculate the expected running time - without having to make assumptions about the probability distribution of inputs.
  • Note that when we

randomised-hire-assistant(n)
    // randomly permute the list of candidates
		for j = 1 to n
        interview candidate j // at cost ci
        if candidate j is better than the best candidate
            best = j
            hire candidate j // at cost ch

• We want a uniform random permutation - $\frac{1}{n!}$ chance of each permutation of the $n$ elements of array $A$

permute-by-sort(A)
    n = A.length
    let P[1..n] be a new array
    for i = 1 to n
        P[i] = random(1, n^3)
    sort A, using P as the sort keys

• This algorithm is guaranteed to give us elements with uniform random distribution given that the keys chosen by the random algorithm are unique.

• The probability of this occurring is given by

  $$\frac{n^3}{n^3}\times \frac{n^3-1}{n^3}\times \frac{n^3-2}{n^3}\times\cdot\times\color{lightblue}\frac{n^3-(n-1)}{n^3}$$

• As a lower bound, we can multiply the last tern $n$ times:

  $$\frac{n^3}{n^3}\times \frac{n^3-1}{n^3}\times \frac{n^3-2}{n^3}\times\cdot\times{\color{lightblue}\frac{n^3-(n-1)}{n^3} \ge ({\color{lightblue}{\frac{n^3-(n-1)}{n^3})^n}}} \\\ge(1-\frac{1}{n^2})^n\ge1-\frac{1}{n}$$

• Chance of succeeding is going to be larger as the value of $n$ increases.

• We can extend the previous example by randomly permuting in place.

  randomise-in-place(A)
      n = A.length
      for i = 1 to n
          swap A[i] <-> A[Random(i, n)]
  

  • This code will produce a given random permutation with probability $\frac{1}{n!}$
  • Proving this may seem tricky, but we can do it using a loop invariant.
  • Terminology: A $k$-permutation of a set of $n$ elements is defined to be the sequence containing $k$ of the $n$ elements.
  • Following this definition, our invariant, denoted $\text{inv(i)}$ is that $A[1..i]$ contains any i-permutation of A with probability $\frac{(n-i)!}{n!}$
  • Upon the loop finishing, we know that we have a given permutation of $A$ with probability $\frac{1}{n!}$

• A loop invariant is a property that is true for:

  • Before we enter the loop body for the first time
  • After each execution of the loop body

• We can prove that this invariant holds using a proof by mathematical induction

• We now prove that the base case holds - the invariant is true when $i=0$, before we enter the loop body.

• Before the first iteration, the array $A[1..0]$ contains a (given) 0-permutation with probability

  $$1=\frac{(n-0)!}{n!}$$

• Given that the invariant holds for $i-1$, $\text{inv}(i-1)$, we want to prove that the invariant holds for $\text{inv}(i)$

  • Assume $A[1...i-1]$ contains any $(i-1)$ permutation with probability $\color{lightgreen}\frac{(n-i+1)!}{n!}$

  • We consider the $i-$permutation $\langle x_1, \cdots , x_i\rangle$

  • Let $E_1$ be the event that $A[1...i-1]$ is $\langle x_1, \cdots, x_{i-1}\rangle$

    • We already know this probability, from the inductive assumption

  • Let $E_2$ be the event that the $i^\text{th}$ iteration places $x_i$ in $A[i]$

    • This probability is given by choosing a specific $x_i$ from the remaining elements.
    • We know that there are $n-i+1$ elements left, and thus the probability is ${\color{lightblue}\frac{1}{n-i+1}}$

  • The probability of the $i-$permutation $\langle x_1, \cdots , x_i\rangle$ occurring is given by the probability of both $E_1$ and $E_2$ occurring:

    $$\begin{aligned} Pr\{E_2\cap E_1\}&=Pr\{E_2|E_1\}\cdot Pr\{E_1\}\\ &=Pr\{E_2|E_1\}\cdot{\color{lightgreen}\frac{(n-i+1)!}{n!}}\\ &={\color{lightblue}\frac{1}{n-i+1}}\cdot{\color{lightgreen}\frac{(n-i+1)!}{n!}}\\ &=\frac{(n-i)!}{n!} \end{aligned}$$

• This is the value that we get for our substitution of $i$ and thus the inductive argument is proven true.

• We now need to prove that the loop does in fact terminate which is easy to argue

• On termination, $\text{inv}(n)$ holds, that is, $A[1..n]$ contains any $n-\text{permutation}$ of the original array, with probability

  $$\frac{(n-n)!}{n!}=\frac{1}{n!}$$

• Therefore A contains any permutation of the original array with probability $\frac{1}{n!}$

• Therefore, each of the possible $n!$ permutations of the original arary is equally likely - a uniform distribution of outcomes.

2.0 - Analysis of Comparison Based Sorting Algos

• Merge Sort Divide and Conquer
• Heap Sort Build and manipulate a heap
• Quick Sort Pre-process array by partitioning into elements greater-than and less-than some elements (the “pivot”)
• Merge-Sort and Heap-Sort have $\Theta(n \lg n)$ worst case time complexity, where Quick-Sort has $\Theta(n^2)$ time complexity.

2.1 - Quick-Sort

• Quick Sort - Pre-process data into “low” and “high” elements.

  quicksort(A, p, r)
      if (p < r)
          q = partition(A, p, r)
          quicksort(A, p, q-1)
          quicksort(A, q+1, r)
  

• All elements from in the subrange $p..q$ are less than elements from $q+1..r$

• Given these two partitions, we recursively call the quicksort algorithm on both sub-partitions

  • Note that these sub-partitions are not of equal size, and thus the time complexity analysis for quick sort is more complicated.

2.1.1 - Partition

• The partition(A, p, r) algorithm rearranges A at the subrange $p..r$ (in place).

• The element $A[r]$ is the pivot value for this example

• In this example, we choose $A[r]=4$ as the pivot

  Partition(A, p, r)
      x = A[r]
      i = p - 1
      for j = p to r - 1
          if A[j] <= x
              i = i + 1
              exchange A[i] with A[j]
      exchange A[i + 1] with A[r]
      return i + 1
  

• We then continue running the algorithm, until everything less than the pivot is to its left, and everything greater than the pivot is to the right.

  

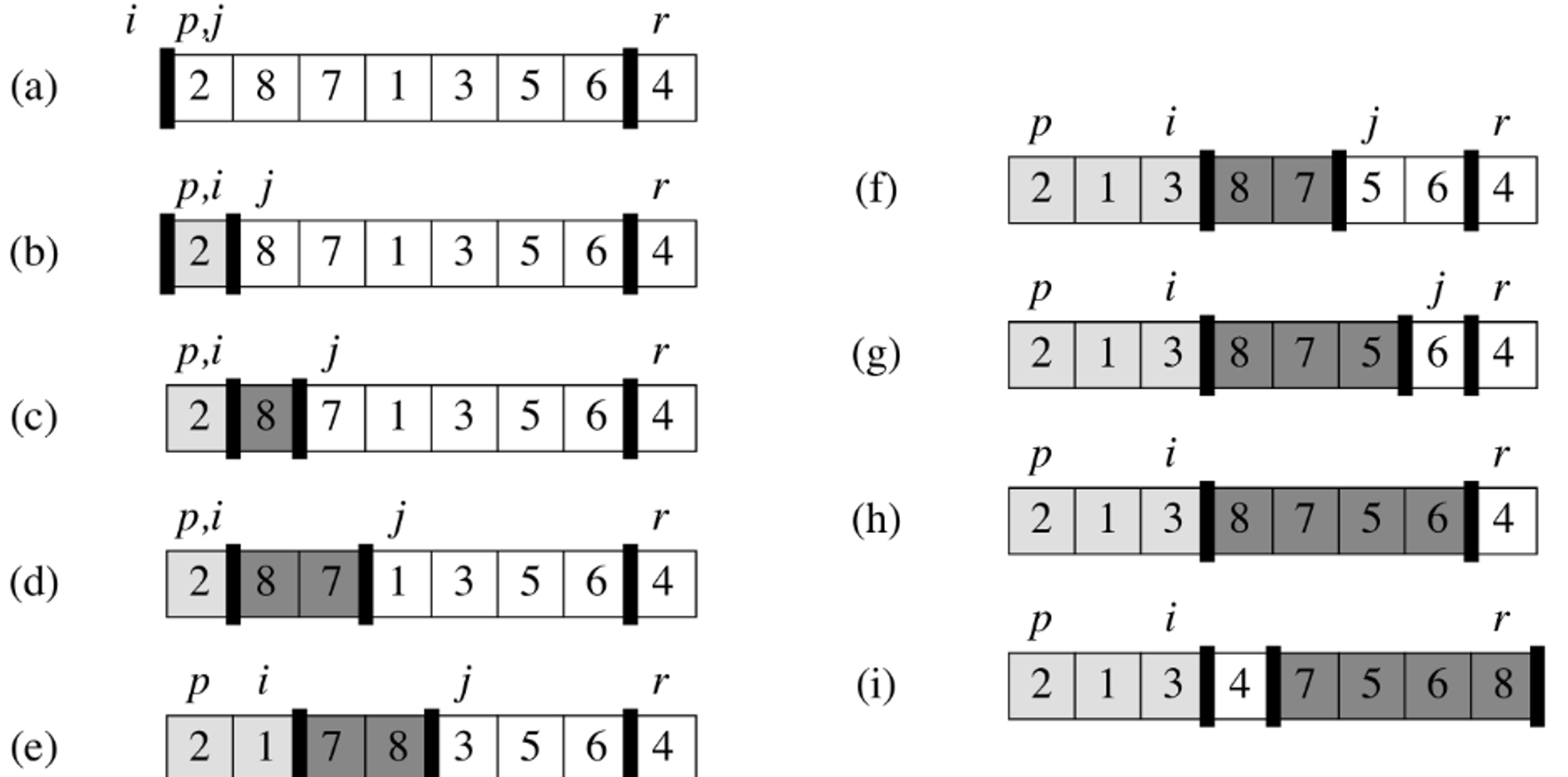
• The partition algorithm keeps track of two indices = $i, j$ which have initial values:

  • $i=p-1$
  • $j=p$

• Initially, the portion of the array from $p\rightarrow i$ and $i\rightarrow j$ will be empty.

• As the algorithm progresses, we maintain the invariant that the elements in $A[p..i]\le x$ and $A[i..j]>x$

  

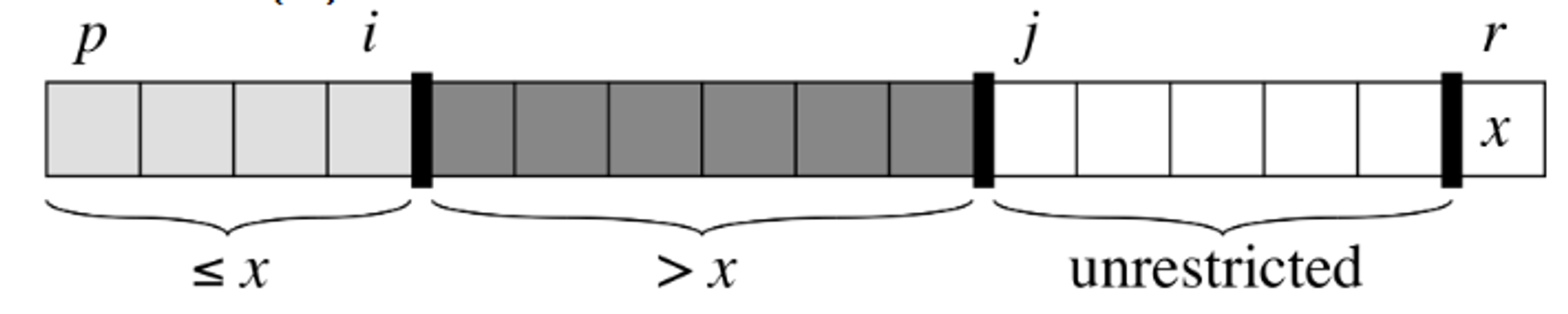
• We maintain the invariant by checking the element $A[j]$ and comparing it with the pivot element, $x$

• If the element is less than or equal to $x$, we place it at the end of the first portion. This overwrites the first element in the portion of elements $>x$ so we place the displaced element where the element we’re inserting came from.

• Otherwise, (if the element is greater than $x$) we don’t need to perform this swapping procedure, and can simply just increment the value of $j$ through the for-loop.

• Upon completing the for-loop iterations, we can insert $r$ in-place between our two partitions

2.2.2 - Analysis of Quick Sort

• The performance of the quick-sort algorithm depends on the element chosen as pivot

  • Best and Average Case $\Theta(n \lg n )$
  • Worst Case $\Theta(n^2)$ = insertion sort

• Worst case occurs when the input array is sorted.

• When array is almost sorted (or is sorted) insertion sort runs in near-linear time.

• The best occurs when $q=\lfloor(p+r)/2\rfloor$ (best case occurs when QuickSort behaves like mergesort)

  $$T(n)=2T(n/2)+\Theta(n)\\ =\Theta(n \lg n)$$

• Constant Ratio Split: $q=p+(r-p)/c$

  $$T(n)=T(\frac{n}{c})+T(\frac{(c-1)n}{c})+\Theta(n)$$

  • That is, consider what happens if we have $\frac{n}{c}$ elements in the first partition and $\frac{(c-1)n}{c}$ in the second partition

    $$T(n)=\Theta(n \lg n)$$

• The worst case occurs when we have one partition with no elements, and thus the call size decreases by 1 each iteration (for the other partition)

  $$T(n)=T(0)+T(n-1)+\Theta(n)$$

  • The worst case is:

  $$\Theta(n^2)$$

2.2.3 - Intuition for “Constant Ratio Split”

• Suppose $c=\frac{1}{10}$

    <figure style="display:flex;justify-content:center;max-width:60%;">
    <img src="./assets/constant-split-ratio.png">
  

• At each level we perform $\Theta(n)$ work

• The upper (or lower) bound on the tree is dependent on the height of the tree

  • Lower bound derived by tracing down the leftmost branch where we reduce by a factor of $\frac{1}{10}$ each time

    $$h\approx \lg_{10} n$$

  • Upper bound derived by tracing down the rightmost branch where we reduce by a factor of $\frac{9}{10}$ each time

    $$h\approx \lg_{\frac{10}{9}} n$$

  • Even in the worst case, we have a time complexity of

    $$\Theta(n \lg n)$$

2.2.4 - Average Case Analysis for Quick-Sort

• Consider the total number of comparisons of elements done by partition over all calls by quicksort.
• Label the elements of A as $z_1, \cdots z_n$ with $z_i$ being the $i^\text{th}$ smallest element.
• Let $Z_{ij}=\{z_i, \cdots, z_j\}$
• Consisting an input array consisting of $1..10$ in any order, and assume that the pivot is 4
• The array is partitioned into two sets:

$$\{1, 2, 3\}\text{ and } \{5, 6, 7, 8, 9, 10\}$$

• In partitioning:
  • The pivot 4 is compared with every element
  • But no element from the first set is (or ever will be) compared with an element from the second set.

**********************Probability $z_i$ compared with $z_j$

• For any elements $z_i$ and $z_j$, once a pivot $x$ is chosen such that

  $$z_i<x<z_j$$

  $z_i$ and $z_j$ can never be compared in the future

• If $z_i$ is chosen as a pivot before any other element in $Z_{ij}$ (that is, $z_i=\min(Z_{ij})$, then $z_i$ will be compared with every other element in $Z_{ij}$

  • Likewise, if $z_j=\max(Z_{ij})$

  • Thus, $z_i$ and $z_j$ are compared if and only if the first element chosen as a pivot in $Z_{ij}$ is either $z_i$ or $z_j$

  • Any element in $Z_{ij}$ is equally likely to be chosen as a pivot and $Z_{ij}$ has $j-i+1$ elements.

  • That is, each element occurs with probability:

    $$\frac{1}{j-1+1}$$

Analysis of Quick Sort

• Each pair of elements is compared at most once because in the partition algorithm, elements are compared with the pivot only at most once, and an element is only used as a pivot in at most one call to partition.

  $$\begin{aligned} &\text{Pr\{}z_i \text{ is compared with }z_j\}\\ =\ &\text{Pr}\{z_i \text{ or } z_j \text{ is the first pivot chosen from } Z_{ij}\}\\ =\ &\text{Pr}\{z_i \text{ is the first pivot chosen from } Z_{ij}\} +\\ &\ \ \ \ \text{Pr\{} z_j \text{ is the first pivot chosen from } Z_{ij}\}\\ =\ &\frac{1}{j-i+1}+\frac{1}{j-i+1}\\ =\ &\frac{2}{j-i+1} \end{aligned}$$

Number of Comparisons over all calls to Partition

• To determine the number of comparisons over all calls to the partition algorithm, we must consider all combinations of $\color{lightblue}i$ and $\color{lightgreen}j$

$$\begin{aligned} &\sum_{{\color{lightblue}i}=1}^{n-1}\sum_{{\color{lightgreen}j}=i+1}^{n}\text{Pr\{}z_i\text{ is compared with } z_j\}\\ =&\sum_{{\color{lightblue}i}=1}^{n-1}\sum_{{\color{lightgreen}j}=i+1}^{n}\frac{2}{j-i+1}\\ =&\sum_{{\color{lightblue}i}=1}^{n-1}\sum_{{\color{lightgreen}j}=i+1}^{n}\frac{2}{k+1},&\text{Let } k = j-i\\ <&\sum_{{\color{lightblue}i}=1}^{n-1}\sum_{k=1}^{n}\frac{2}{k}\\ =&\sum_{{\color{lightblue}i}=1}^{n-1}O(\lg n ),&\text{Harmonic Series}\\ =&O(n \lg n) \end{aligned}$$

2.2.5 - Randomised Quick-Sort

• Despite the bad worst-case bound, Quicksort is regarded by many to be a good sorting algorithm
• Good expected-case performance can be achieved by randomly permuting the input before sorting.
  • This permuting can be done in $\Theta(n)$
• In practice, an even simpler approach specific to QuickSort is to choose a pivot from a random location.
  • This just requires a constant-time swap of some random element $A[i]$ with $A[r]$
• Having done this, the worst-case is unlikely, and the expected time complexity of the algorithm becomes $\Theta(n \lg n)$

2.2 - Merge Sort

• Merge Sort - post-process sorted data into a single, sorted array

  merge-sort(A, p, r)
      if (p < r)
           q = floor((p+r)/2)
           merge-sort(A, p, q)
           merge-sort(A, q+1, r)
           merge(A, p, q, r)
  

• Sort then post-process (merge)

• At each stage, we’re calling merge-sort on subproblems that are exactly half the size.

• Thus, the recurrence that describes this algorithm’s running time is:

  $$T(n)=2T(\frac{n}{2}) + \Theta(n)\\ =\Theta(n \lg n)$$

3.0 - Randomised Algorithm Example

💡 Given a procedure, biased-random() that returns 0 with probability $p$ and $1$ with probability $1-p$, where $0<p<1$, how can you implement a procedure $\text{random}$ that returns 0 or 1 with equal probability

3.1 - Algorithm Construction

random()
    a = biased-random()

• Flipping the coin once gives the following:

  • $P(a==0) =p$
  • $P(a==1)=1-p$

• Flipping the coin twice gives the following

  • $P(a=0\wedge b=0)=p^2$
  • $P(a=0\wedge b=1)=p\times (1-p)$
  • $P(a=1\wedge b=0)=p\times (1-p)$
  • $P(a=1\wedge b=1)=(1-p)^2$

• Thus,

  $$\begin{aligned} P(a=0\wedge a\ne b)&=\frac{p\times (1-p)}{p\times (1-p) + p\times (1-p)}\\ &=\frac{1}{2} \end{aligned}$$

• Finally, our algorithm is:

  Random()
      a = biased-random()
      b = biased-random()
      while a == b:
          a = biased-random()
          b = biased-random()
      return a
  

• This algorithm has almost-certain termination, but there is a probability that it continues forever (with probability $\approx 0$)

3.2 - Expected Running Time

• We can count the expected running time of the algorithm as a function of the number of times that it runs.

• Let $\alpha=2(p\times (1-p))$ be the probability that $a\ne b$

• Probability of terminating after 0 loop iterations is $\alpha$

  • That is, our first coin flip yields our desired result.

• Probability of terminating after 1 loop iterations is $(1-\alpha)\times \alpha$

  • $(1-\alpha)$ is the probability of a “bad” flip occurring

• Probability of terminating after 2 loop iterations is $(1-\alpha)^2\times\alpha$

• Probability of terminating after $i$ loop iterations is $(1-\alpha)^i\times\alpha$

• Using this result, the expected number of loop iterations is

  $$\begin{aligned} &\sum_{i=0}^\infty i\times ((1-\alpha)^i\times\alpha)\\ =&\alpha\times(\sum_{i=0}^\infty i \times ((1-\alpha)^i))\\ =&\alpha\times\frac{1-\alpha}{(1-(1-\alpha))^2}\\ =&\alpha\times\frac{1-\alpha}{\alpha^2}\\ =&\frac{1}{\alpha}-1 \end{aligned}$$

• If $\alpha=\frac{1}{2}$ then we would expect to perform 1 iteration

• The more unfair our coin gets, the more iterations we expect to perform